接線の方程式
Follow @tepika_math接線の傾きは求まった!!!
$\displaystyle{y=x^2}$ のグラフと、
このグラフの$\displaystyle{x=1}$での点での接線を、
以下に描きます。
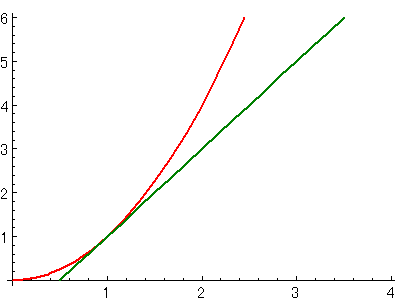
さて、この緑色で描かれた、接線の傾きはいくつでしょうか?
今までのことを振り返れば、すぐに分かると思います。
そう、微分です!!!
このグラフ$\displaystyle{y=x^2}$を微分すると、
$\displaystyle{y'=2x}$と導関数が求まりますので、
この導関数に$\displaystyle{x=1}$を代入したら、結果は2となり、接線の傾きは2となります。
ところで、導関数に値を代入したもの、つまり、
$\displaystyle{f'(a)}$のような形のこと(この場合、xに定数aを代入した)を、
$\displaystyle{f(x)}$の$\displaystyle{x=a}$における微分係数といいます。
微分係数という言葉は案外忘れやすいと思うので、しっかりと覚えておきましょう。
上のグラフでいうと、 $\displaystyle{y}$の$\displaystyle{x=1}$における微分係数は2となる、ということです。
つまり、微分係数とは、接線の傾きの値そのものです。
このグラフの$\displaystyle{x=1}$での点での接線を、
以下に描きます。

さて、この緑色で描かれた、接線の傾きはいくつでしょうか?
今までのことを振り返れば、すぐに分かると思います。
そう、微分です!!!
このグラフ$\displaystyle{y=x^2}$を微分すると、
$\displaystyle{y'=2x}$と導関数が求まりますので、
この導関数に$\displaystyle{x=1}$を代入したら、結果は2となり、接線の傾きは2となります。
ところで、導関数に値を代入したもの、つまり、
$\displaystyle{f'(a)}$のような形のこと(この場合、xに定数aを代入した)を、
$\displaystyle{f(x)}$の$\displaystyle{x=a}$における微分係数といいます。
微分係数という言葉は案外忘れやすいと思うので、しっかりと覚えておきましょう。
上のグラフでいうと、 $\displaystyle{y}$の$\displaystyle{x=1}$における微分係数は2となる、ということです。
つまり、微分係数とは、接線の傾きの値そのものです。
接線の方程式は?
接線の傾きは確かに求めることができました。
でも、接線の方程式は?
接線といえど、一応直線です。
ところで直線の式といえば、中学で習った形、
$\displaystyle{y=ax+b}$
でしたよね??
aを傾き、bを切片というのでした。
だから、傾きaを求めただけでは、方程式はできたとは言えません。
ちゃんと、切片bも求めましょう。
それでは、関数$\displaystyle{f(x)}$の、
点$\displaystyle{(a,f(a))}$での、接線の方程式を求めましょう。
当然、傾きは$\displaystyle{f'(a)}$となります。
よって、切片を$\displaystyle{b}$とすると、接線のグラフの式は
$\displaystyle{y=f'(a)x+b}$
となります。
あとは、中学数学の知識を使えば、切片を求めることもできますね?
この接線が 点$\displaystyle{(a,f(a))}$を通ることを利用して、
$\displaystyle{(x,y)=(a,f(a))}$を代入すればよいのです。
そうすると、
$\displaystyle{f(a)=f'(a)a+b}$となり、
$\displaystyle{b=f(a)-f'(a)a}$となるので、
これで切片bが求まりました。
これで、傾きと切片が求まったので、直線の式は、
$\displaystyle{y=f'(a)x+f(a)-f'(a)a}$$\displaystyle{\cdots\cdots(1)}$
となります。
ところで教科書では、
接線の方程式は(1)の代わりに次のような形で出てくることがほとんどです。
$\displaystyle{y-f(a)=f'(a)(x-a)}$$\displaystyle{\cdots\cdots(2)}$
(2)の右辺を展開して、左辺の第二項目を右辺に移項したら(1)の形になりますので、
(1)も(2)も全く同じことです。
どちらにしろ、接線の方程式は、自分で求めるよりも、
(1)と(2)どちらでもよいので、覚えておいた方がよいです。
よく試験では「接線の方程式を求めよ」というような問題が出てきますが、
試験は時間勝負ですので、接線の方程式をいちいち導くよりは、公式として覚えておいた方が
最も効率がよいと思います。
でも、接線の方程式は?
接線といえど、一応直線です。
ところで直線の式といえば、中学で習った形、
$\displaystyle{y=ax+b}$
でしたよね??
aを傾き、bを切片というのでした。
だから、傾きaを求めただけでは、方程式はできたとは言えません。
ちゃんと、切片bも求めましょう。
それでは、関数$\displaystyle{f(x)}$の、
点$\displaystyle{(a,f(a))}$での、接線の方程式を求めましょう。
当然、傾きは$\displaystyle{f'(a)}$となります。
よって、切片を$\displaystyle{b}$とすると、接線のグラフの式は
$\displaystyle{y=f'(a)x+b}$
となります。
あとは、中学数学の知識を使えば、切片を求めることもできますね?
この接線が 点$\displaystyle{(a,f(a))}$を通ることを利用して、
$\displaystyle{(x,y)=(a,f(a))}$を代入すればよいのです。
そうすると、
$\displaystyle{f(a)=f'(a)a+b}$となり、
$\displaystyle{b=f(a)-f'(a)a}$となるので、
これで切片bが求まりました。
これで、傾きと切片が求まったので、直線の式は、
$\displaystyle{y=f'(a)x+f(a)-f'(a)a}$$\displaystyle{\cdots\cdots(1)}$
となります。
ところで教科書では、
接線の方程式は(1)の代わりに次のような形で出てくることがほとんどです。
$\displaystyle{y-f(a)=f'(a)(x-a)}$$\displaystyle{\cdots\cdots(2)}$
(2)の右辺を展開して、左辺の第二項目を右辺に移項したら(1)の形になりますので、
(1)も(2)も全く同じことです。
どちらにしろ、接線の方程式は、自分で求めるよりも、
(1)と(2)どちらでもよいので、覚えておいた方がよいです。
よく試験では「接線の方程式を求めよ」というような問題が出てきますが、
試験は時間勝負ですので、接線の方程式をいちいち導くよりは、公式として覚えておいた方が
最も効率がよいと思います。