接線の傾きを求めよう
Follow @tepika_math接線の確認
接線ってなんだっけ?(・ω・)ノ
・・・ってな人のために、もう一回接線について確認していきたいと思います。
下のグラフを見てください↓↓↓
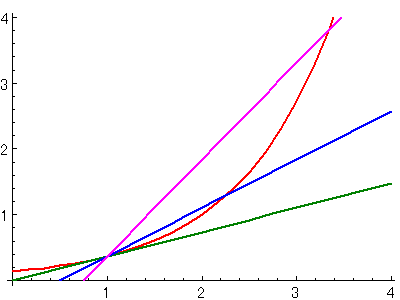
このグラフには、赤色の曲線1つとピンク・青・緑の3つの直線があります。
ピンクと青の直線を見てください。
この2つの直線は赤色の曲線をぐさっと貫通して走っているのが分かると思います。
しかし、緑色の直線はどうでしょうか?
曲線を突き抜けているわけでもない、だからといって曲線から離れているわけでもない・・・
という、ちょうどいい位置にいます。
本当に曲線に「くっついている」ような状態のことです。
このような、曲線から離れているわけでも貫通しているわけでもない、
ただ「くっついている」ような直線のことを、
その曲線の接線と言います。
・・・ってな人のために、もう一回接線について確認していきたいと思います。
下のグラフを見てください↓↓↓

このグラフには、赤色の曲線1つとピンク・青・緑の3つの直線があります。
ピンクと青の直線を見てください。
この2つの直線は赤色の曲線をぐさっと貫通して走っているのが分かると思います。
しかし、緑色の直線はどうでしょうか?
曲線を突き抜けているわけでもない、だからといって曲線から離れているわけでもない・・・
という、ちょうどいい位置にいます。
本当に曲線に「くっついている」ような状態のことです。
このような、曲線から離れているわけでも貫通しているわけでもない、
ただ「くっついている」ような直線のことを、
その曲線の接線と言います。
接線の傾きを求めてみよう
それでは、$\displaystyle{f(x)=x^2}$の、$\displaystyle{x=1}$での、接線の傾きを求めてみましょう。
このときの接線は、以下の緑の直線になると思います。
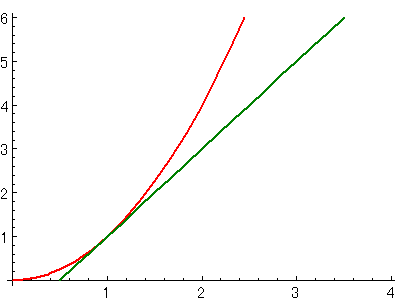
ちょっと見にくいとは思いますが(申し訳ない。。。m(_ _)mペコリ)
$\displaystyle{x=1}$で緑の直線が赤の曲線に接していると思います。
さて、緑色の直線の傾きを求めたいわけですが・・・
ところで、傾きの求め方は覚えていますか?
です。
この接線の傾きを求めるにはどうしたらよいでしょうか?
それには、まず以下のグラフを考えましょう。
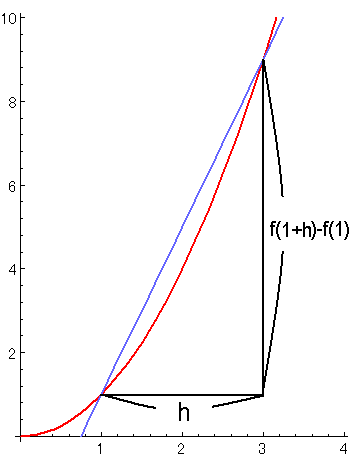
この場合、青色の直線は、接線とは大きく異なっています。
曲線と、2つの点で交わっているため、接線ではありません。
それでもおかまいなしに、この接線ではない直線の傾きを求めることにしましょうか。
グラフに書いてあるように、
この2つの点の間のx方向の距離を$\displaystyle{h}$とします。
そうすると、2つの点のy方向の距離は
$\displaystyle{f(1+h)-f(1)}$
つまり、
$\displaystyle{(1+h)^2-1}$
となります。
よって、この青色の直線の傾きは、
$\displaystyle{\frac{(1+h)^2-1}{h}}$ となります。
ってこの青色の直線は接線じゃないから、求めても意味がないだろ。。。
もしそう思ったら、この2点の交点の距離、つまりhをどんどん小さくしてみましょう。
以下のグラフを見てください。
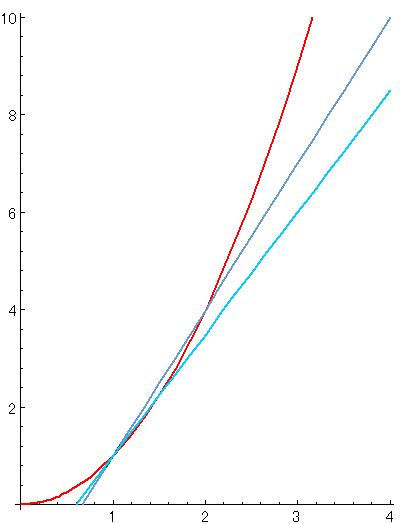
このように、2つの交点の距離、つまりhをどんどん0に近づけたら、接線に近づいていくことが分かりませんか?
そう、接線の傾きを求めるのに「極限値」を用いれば、よさそうです。
$\displaystyle{f(x)=x^2}$の、$\displaystyle{x=1}$での、接線の傾きは、
極限値を使うと、
$\displaystyle{\lim_{h{\rightarrow}0}\frac{(1+h)^2-1}{h}}$となります。
この極限値を解くと、
$\displaystyle{=\lim_{h{\rightarrow}0}\frac{h^2+2h+1-1}{h}=\lim_{h{\rightarrow}0}\frac{h^2+2h}{h}=\lim_{h{\rightarrow}0}(h+2)=2}$
となり、この接線の傾きは2であることが分かりました。
このときの接線は、以下の緑の直線になると思います。

ちょっと見にくいとは思いますが(申し訳ない。。。m(_ _)mペコリ)
$\displaystyle{x=1}$で緑の直線が赤の曲線に接していると思います。
さて、緑色の直線の傾きを求めたいわけですが・・・
ところで、傾きの求め方は覚えていますか?
|
=傾き |
です。
この接線の傾きを求めるにはどうしたらよいでしょうか?
それには、まず以下のグラフを考えましょう。

この場合、青色の直線は、接線とは大きく異なっています。
曲線と、2つの点で交わっているため、接線ではありません。
それでもおかまいなしに、この接線ではない直線の傾きを求めることにしましょうか。
グラフに書いてあるように、
この2つの点の間のx方向の距離を$\displaystyle{h}$とします。
そうすると、2つの点のy方向の距離は
$\displaystyle{f(1+h)-f(1)}$
つまり、
$\displaystyle{(1+h)^2-1}$
となります。
よって、この青色の直線の傾きは、
$\displaystyle{\frac{(1+h)^2-1}{h}}$ となります。
ってこの青色の直線は接線じゃないから、求めても意味がないだろ。。。
もしそう思ったら、この2点の交点の距離、つまりhをどんどん小さくしてみましょう。
以下のグラフを見てください。

このように、2つの交点の距離、つまりhをどんどん0に近づけたら、接線に近づいていくことが分かりませんか?
そう、接線の傾きを求めるのに「極限値」を用いれば、よさそうです。
$\displaystyle{f(x)=x^2}$の、$\displaystyle{x=1}$での、接線の傾きは、
極限値を使うと、
$\displaystyle{\lim_{h{\rightarrow}0}\frac{(1+h)^2-1}{h}}$となります。
この極限値を解くと、
$\displaystyle{=\lim_{h{\rightarrow}0}\frac{h^2+2h+1-1}{h}=\lim_{h{\rightarrow}0}\frac{h^2+2h}{h}=\lim_{h{\rightarrow}0}(h+2)=2}$
となり、この接線の傾きは2であることが分かりました。
接線の傾きの求め方
基本的に、関数$\displaystyle{f(x)}$の点$\displaystyle{x}$での接線の傾きは、以下のグラフのようになります。
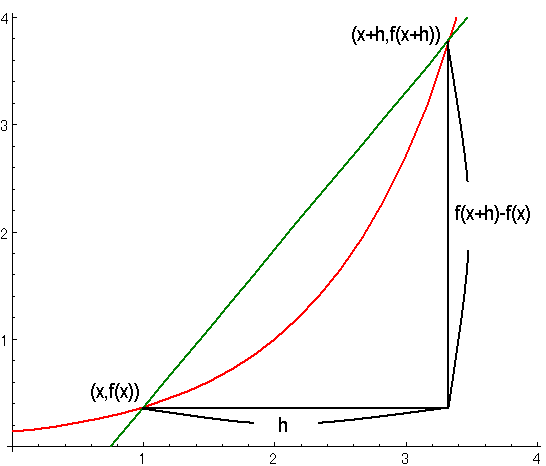
見て分かるように、$\displaystyle{x}$の増加量が$\displaystyle{h}$のとき、
$\displaystyle{y}$の増加量は$\displaystyle{f(x+h)-f(x)}$となります。
この$\displaystyle{h}$をどんどん小さくしていく感覚で、接線の傾きを求めることができます。
$\displaystyle{\lim_{h{\rightarrow}0}\frac{f(x+h)-f(x)}{h}}$
となります。

見て分かるように、$\displaystyle{x}$の増加量が$\displaystyle{h}$のとき、
$\displaystyle{y}$の増加量は$\displaystyle{f(x+h)-f(x)}$となります。
この$\displaystyle{h}$をどんどん小さくしていく感覚で、接線の傾きを求めることができます。
$\displaystyle{\lim_{h{\rightarrow}0}\frac{f(x+h)-f(x)}{h}}$
となります。