極大値と極小値
Follow @tepika_math極大値と極小値
微分したら、
どの区間が、右上がりor右下がりなのか、ということが分かるようになり、
そこからグラフの概形を知ることができました。
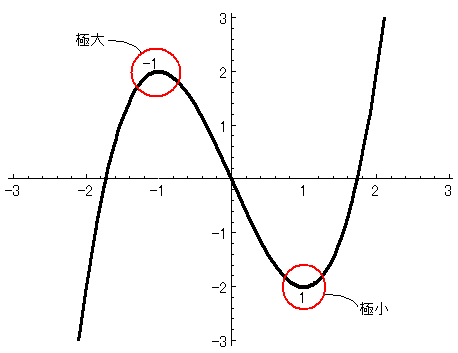
以下に再び、$\displaystyle{y=x^3-3x}$のグラフを示します。
ここで、重要語句を挙げたいと思います。
この、赤い丸で囲んだ、山になっている点を極大といいます。
また同じように、赤い丸で囲んだ谷になっている点を極小といいます。
また、このときの$\displaystyle{y}$の値のことを極大値、または極小値といいます。
極大値と極小値をまとめて極値といいます。
つまり、極大とは、いったん値が大きくなっている所であり、
同じく極小とは、いったん値が小さくなっている所です。
このグラフを見ると、
$\displaystyle{x=-1}$のとき、$\displaystyle{y}$が極大値になっていて、
$\displaystyle{x=1}$のとき、$\displaystyle{y}$が極小値になっています。
さて、これらの極値を求めましょう。
このグラフの式は、
$\displaystyle{y=x^3-3x}$
なので、この$\displaystyle{x}$に1と−1をそれぞれ代入すれば、
その極値が求まります。
実際に代入してみると、
$\displaystyle{x=-1}$のとき、$\displaystyle{y}$は極大値$\displaystyle{2}$をとり、
$\displaystyle{x=1}$のとき、$\displaystyle{y}$は極小値$\displaystyle{-2}$をとります。
どの区間が、右上がりor右下がりなのか、ということが分かるようになり、
そこからグラフの概形を知ることができました。
以下に再び、$\displaystyle{y=x^3-3x}$のグラフを示します。

ここで、重要語句を挙げたいと思います。
この、赤い丸で囲んだ、山になっている点を極大といいます。
また同じように、赤い丸で囲んだ谷になっている点を極小といいます。
また、このときの$\displaystyle{y}$の値のことを極大値、または極小値といいます。
極大値と極小値をまとめて極値といいます。
つまり、極大とは、いったん値が大きくなっている所であり、
同じく極小とは、いったん値が小さくなっている所です。
このグラフを見ると、
$\displaystyle{x=-1}$のとき、$\displaystyle{y}$が極大値になっていて、
$\displaystyle{x=1}$のとき、$\displaystyle{y}$が極小値になっています。
さて、これらの極値を求めましょう。
このグラフの式は、
$\displaystyle{y=x^3-3x}$
なので、この$\displaystyle{x}$に1と−1をそれぞれ代入すれば、
その極値が求まります。
実際に代入してみると、
$\displaystyle{x=-1}$のとき、$\displaystyle{y}$は極大値$\displaystyle{2}$をとり、
$\displaystyle{x=1}$のとき、$\displaystyle{y}$は極小値$\displaystyle{-2}$をとります。
極値になるためには!?
極大値や極小値は分かりましたか?
極大値とは、グラフで山になっている部分の値であり、
極小値とは、グラフで谷になっている部分の値です。
さて、今回は、この「山・谷になっている」というのはどういうことなのか、
ということをもう少し考えてみましょう・・・。
「山や谷になっている」ということは・・・
“グラフの増減”が変わっていることになります。
もっと具体的に言うと、
右上がり、から、右下がりに変わる(極大の場合)
または
右下がり、から、右上がりに変わる(極小の場合)
ということになります。
それは、導関数の+−の符号が変わるということです。
だから、導関数の値がその点では、符号の変わり目となるはずなので、
結局0になるはずです。
つまり、極値ではその点での微分係数が0になるということです。
もう一度、極値の部分を見てください。
グラフの増減がいったん止まっていることが分かります。
グラフの増減が止まっているということは、その点での接線はx軸と平行なため、傾きは0になります。
もう一度言いますと、
極値では、その点での微分係数が0になります。
だから、極値を見つけたかったら微分係数が0になる点を探せばよいわけです。
例えば、$\displaystyle{y=x^3-3x}$のグラフでは、
極値は$\displaystyle{x=-1}$と$\displaystyle{x=1}$になりますが、
このグラフの導関数$\displaystyle{y'=3x^2-3}$に、
極値である$\displaystyle{x=-1}$と$\displaystyle{x=1}$を代入しますと、
確かに0となります!!
極大値とは、グラフで山になっている部分の値であり、
極小値とは、グラフで谷になっている部分の値です。
さて、今回は、この「山・谷になっている」というのはどういうことなのか、
ということをもう少し考えてみましょう・・・。
「山や谷になっている」ということは・・・
“グラフの増減”が変わっていることになります。
もっと具体的に言うと、
右上がり、から、右下がりに変わる(極大の場合)
または
右下がり、から、右上がりに変わる(極小の場合)
ということになります。
それは、導関数の+−の符号が変わるということです。
だから、導関数の値がその点では、符号の変わり目となるはずなので、
結局0になるはずです。
つまり、極値ではその点での微分係数が0になるということです。
もう一度、極値の部分を見てください。
グラフの増減がいったん止まっていることが分かります。
グラフの増減が止まっているということは、その点での接線はx軸と平行なため、傾きは0になります。
もう一度言いますと、
極値では、その点での微分係数が0になります。
だから、極値を見つけたかったら微分係数が0になる点を探せばよいわけです。
例えば、$\displaystyle{y=x^3-3x}$のグラフでは、
極値は$\displaystyle{x=-1}$と$\displaystyle{x=1}$になりますが、
このグラフの導関数$\displaystyle{y'=3x^2-3}$に、
極値である$\displaystyle{x=-1}$と$\displaystyle{x=1}$を代入しますと、
確かに0となります!!
極値を持つとは限らない!?
前回は、極値の場合、その点での微分係数が0になると言いました。
それならば、微分係数が0の点は、絶対に極値でしょうか?
・・・実はそうとは限りません。。。
つまり、
$\displaystyle{x=a}$で$\displaystyle{y}$が極値$\displaystyle{\Rightarrow}$$\displaystyle{x=a}$での微分係数が0
・・・というのは確かに成立します。
しかし、
$\displaystyle{x=a}$での微分係数が0$\displaystyle{\Rightarrow}$$\displaystyle{x=a}$で$\displaystyle{y}$が極値
となるとは、必ずしも言えないということです。
つまり、逆が成り立つとは限らないのです。
逆が成り立たない例として、
$\displaystyle{y=x^3+2}$のような関数のグラフを考えましょう。
さて、このグラフの増減表は以下のようになります。
だから、このグラフは以下のようになります。
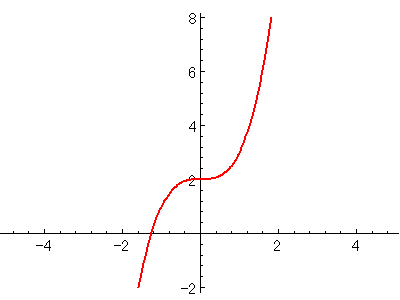
このグラフは、確かにx=0で微分係数が0です。
グラフを見れば、増加がこの点で緩やかになっているようにも見えますが、
山や谷になっているわけじゃないので、極値ではないです。
つまり、極値は実際に微分してみて
増減表を用いてグラフを描いてみないと
分からないわけですね・・・。
それならば、微分係数が0の点は、絶対に極値でしょうか?
・・・実はそうとは限りません。。。
つまり、
$\displaystyle{x=a}$で$\displaystyle{y}$が極値$\displaystyle{\Rightarrow}$$\displaystyle{x=a}$での微分係数が0
・・・というのは確かに成立します。
しかし、
$\displaystyle{x=a}$での微分係数が0$\displaystyle{\Rightarrow}$$\displaystyle{x=a}$で$\displaystyle{y}$が極値
となるとは、必ずしも言えないということです。
つまり、逆が成り立つとは限らないのです。
逆が成り立たない例として、
$\displaystyle{y=x^3+2}$のような関数のグラフを考えましょう。
さて、このグラフの増減表は以下のようになります。
| $\displaystyle{x}$ | $\displaystyle{\cdots}$ | $\displaystyle{0}$ | $\displaystyle{\cdots}$ |
|---|---|---|---|
| $\displaystyle{y'}$ | $\displaystyle{+}$ | $\displaystyle{0}$ | $\displaystyle{+}$ |
| $\displaystyle{y}$ | $\displaystyle{\nearrow}$ | $\displaystyle{2}$ | $\displaystyle{\nearrow}$ |

このグラフは、確かにx=0で微分係数が0です。
グラフを見れば、増加がこの点で緩やかになっているようにも見えますが、
山や谷になっているわけじゃないので、極値ではないです。
つまり、極値は実際に微分してみて
増減表を用いてグラフを描いてみないと
分からないわけですね・・・。
まとめ
じゃあ、微分係数が0になっても極値になるとは限らないんだったら、
この判定法はあまり役に立たないのでは・・・
・・・でも大丈夫です。
確かに微分係数が0となっても、極値になるとは限りませんが、
極値では、絶対にその微分係数が0になります。
極値だけど、微分係数が0にならない、ということはまずありません!!!
だから、微分係数が0の場所を見つければ、
とりあえず極値とは限らないけれども、極値の「候補」が全て見つかります。
だから、微分係数が0の場所を見つけるということは、
極値の候補を見つける上で、とても大切なことだと思います。
この判定法はあまり役に立たないのでは・・・
・・・でも大丈夫です。
確かに微分係数が0となっても、極値になるとは限りませんが、
極値では、絶対にその微分係数が0になります。
極値だけど、微分係数が0にならない、ということはまずありません!!!
だから、微分係数が0の場所を見つければ、
とりあえず極値とは限らないけれども、極値の「候補」が全て見つかります。
だから、微分係数が0の場所を見つけるということは、
極値の候補を見つける上で、とても大切なことだと思います。