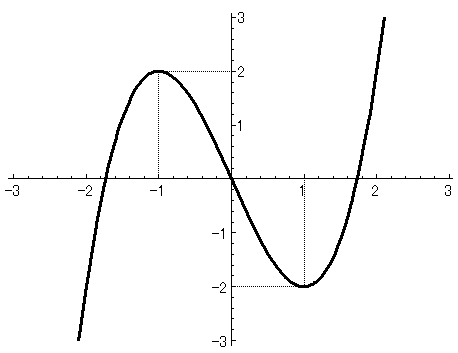グラフの概形
Follow @tepika_mathグラフのおおまかな形
概形とは、おおざっぱな形のことです。
微分とは、接線の傾きを調べるものでした。
また、
接線の傾きが正ならば、その部分では右上がりですし、
接線の傾きが負ならば、その部分では右下がりです。
だから、微分をするとグラフの増減を知ることができるので、
そこから大まかなグラフの形を調べよう、というのが今回のテーマです。
微分とは、接線の傾きを調べるものでした。
また、
接線の傾きが正ならば、その部分では右上がりですし、
接線の傾きが負ならば、その部分では右下がりです。
だから、微分をするとグラフの増減を知ることができるので、
そこから大まかなグラフの形を調べよう、というのが今回のテーマです。
まずは二次関数のグラフから
例えば、
$\displaystyle{y=x^2}$
のような二次関数のグラフで考えてみましょう。
この関数を微分すると、
$\displaystyle{y'=2x}$
となります。
ところで、この導関数は一次関数なので、直線になります。
また、
$\displaystyle{x{\gt}0}$のとき、$\displaystyle{y'}$は 正の値をとり、
逆に
$\displaystyle{x{\lt}0}$のとき、$\displaystyle{y'}$は負の値をとります。
ところで以前にも解説したように、
導関数は接線の傾きを表しているので、
$\displaystyle{x{\gt}0}$のとき、接線の傾きは正でグラフは右上がり、
また
$\displaystyle{x{\lt}0}$のとき、接線の傾きは負でグラフは右下がりになります。
だから$\displaystyle{y=x^2}$のグラフは、以下のような放物線になるのですねo(^^)o
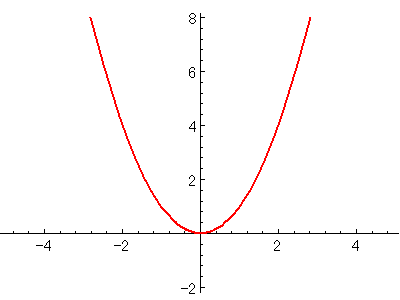
$\displaystyle{y=x^2}$
のような二次関数のグラフで考えてみましょう。
この関数を微分すると、
$\displaystyle{y'=2x}$
となります。
ところで、この導関数は一次関数なので、直線になります。
また、
$\displaystyle{x{\gt}0}$のとき、$\displaystyle{y'}$は 正の値をとり、
逆に
$\displaystyle{x{\lt}0}$のとき、$\displaystyle{y'}$は負の値をとります。
ところで以前にも解説したように、
導関数は接線の傾きを表しているので、
$\displaystyle{x{\gt}0}$のとき、接線の傾きは正でグラフは右上がり、
また
$\displaystyle{x{\lt}0}$のとき、接線の傾きは負でグラフは右下がりになります。
だから$\displaystyle{y=x^2}$のグラフは、以下のような放物線になるのですねo(^^)o

3次関数のグラフ
今回は3次関数のグラフを調べましょう。
ところで、中学で習ってきたことを振り返ってみると、
一次関数のグラフは直線になりました。
二次関数のグラフは放物線になりました。
三次関数のグラフは、一体どんな形になるのでしょうか?
例として、
$\displaystyle{y=x^3-3x}$
のような、3次関数を考えましょう。
さて、これを微分してみますと、
$\displaystyle{y'=3x^2-3=3(x+1)(x-1)}$
となります。
以下に、$\displaystyle{y=3(x+1)(x-1)}$のグラフを示します↓↓
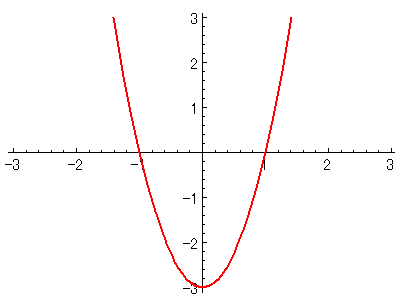
このグラフから、
$\displaystyle{x{\lt}-1,1{\lt}x}$のとき、$\displaystyle{y'}$は 正の値をとり、
$\displaystyle{-1{\lt}x{\lt}1}$のとき、$\displaystyle{y'}$は負の値をとることが分かります。
それから、さっきも書いた通り、
「微分した時の値が正であればグラフは右上がり、負であればグラフは右下がり」
であるので、
$\displaystyle{x{\lt}-1,1{\lt}x}$のとき、$\displaystyle{y}$は右上がりであり、
$\displaystyle{-1{\lt}x{\lt}1}$のとき、$\displaystyle{y}$は右下がりであることが想像できると思います。
ところで、中学で習ってきたことを振り返ってみると、
一次関数のグラフは直線になりました。
二次関数のグラフは放物線になりました。
三次関数のグラフは、一体どんな形になるのでしょうか?
例として、
$\displaystyle{y=x^3-3x}$
のような、3次関数を考えましょう。
さて、これを微分してみますと、
$\displaystyle{y'=3x^2-3=3(x+1)(x-1)}$
となります。
以下に、$\displaystyle{y=3(x+1)(x-1)}$のグラフを示します↓↓

このグラフから、
$\displaystyle{x{\lt}-1,1{\lt}x}$のとき、$\displaystyle{y'}$は 正の値をとり、
$\displaystyle{-1{\lt}x{\lt}1}$のとき、$\displaystyle{y'}$は負の値をとることが分かります。
それから、さっきも書いた通り、
「微分した時の値が正であればグラフは右上がり、負であればグラフは右下がり」
であるので、
$\displaystyle{x{\lt}-1,1{\lt}x}$のとき、$\displaystyle{y}$は右上がりであり、
$\displaystyle{-1{\lt}x{\lt}1}$のとき、$\displaystyle{y}$は右下がりであることが想像できると思います。
増減
さて、このことを以下の増減表に書き込んでみたいと思います。
一番上の列は変数$\displaystyle{x}$を表します。
二番目の列は、$\displaystyle{y}$を微分したときの値が正の値をとるか負の値をとるか、
または0になるかを表しています。
そして、三番目の列は、実際の$\displaystyle{y}$の増減を矢印で表しています。
例えば、$\displaystyle{x}$が−1より小さい時、(左から二番目の行)は、 $\displaystyle{y'}$がプラスなため、
グラフが右上がりになっています。
このことを、三番目の$\displaystyle{y}$の列では、左上の矢印$\displaystyle{\nearrow}$で書かれています。
このようにグラフの概形を調べたい時は、増減表を書くのが一般的です。
この増減表により、$\displaystyle{y=x^3-3x}$のグラフは、だいたい以下のような形になると想像できます。
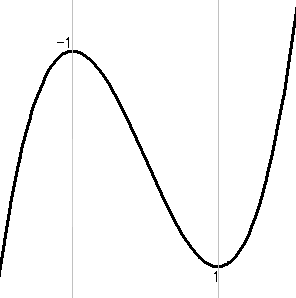
どうですか?こグラフは!!??
これが3次関数のグラフです。
なんだか変わった形ですネ(笑)
最初は、上がったと思ったら、下がり出して、
かと思えば、また上がりだして・・・
| $\displaystyle{x}$ | $\displaystyle{\cdots}$ | $\displaystyle{-1}$ | $\displaystyle{\cdots}$ | $\displaystyle{1}$ | $\displaystyle{\cdots}$ |
|---|---|---|---|---|---|
| $\displaystyle{y'}$ | $\displaystyle{+}$ | $\displaystyle{0}$ | $\displaystyle{-}$ | $\displaystyle{0}$ | $\displaystyle{+}$ |
| $\displaystyle{y}$ | $\displaystyle{\nearrow}$ | $\displaystyle{\searrow}$ | $\displaystyle{\nearrow}$ |
一番上の列は変数$\displaystyle{x}$を表します。
二番目の列は、$\displaystyle{y}$を微分したときの値が正の値をとるか負の値をとるか、
または0になるかを表しています。
そして、三番目の列は、実際の$\displaystyle{y}$の増減を矢印で表しています。
例えば、$\displaystyle{x}$が−1より小さい時、(左から二番目の行)は、 $\displaystyle{y'}$がプラスなため、
グラフが右上がりになっています。
このことを、三番目の$\displaystyle{y}$の列では、左上の矢印$\displaystyle{\nearrow}$で書かれています。
このようにグラフの概形を調べたい時は、増減表を書くのが一般的です。
この増減表により、$\displaystyle{y=x^3-3x}$のグラフは、だいたい以下のような形になると想像できます。

どうですか?こグラフは!!??
これが3次関数のグラフです。
なんだか変わった形ですネ(笑)
最初は、上がったと思ったら、下がり出して、
かと思えば、また上がりだして・・・
もう少し正確に求めましょう
このようにして、グラフの概形を得ることができます。
しかし、もう少しだけ正確に描きたいものです。
せめて、
$\displaystyle{x=-1}$と$\displaystyle{x=1}$は、グラフの増減が変わる点でもあるので、
その点での座標を求めたいものです。
この点はもとのグラフ、
$\displaystyle{y=x^3-3x}$に$\displaystyle{x=-1}$と$\displaystyle{x=1}$を代入すれば、すぐに分かります。
代入してみると、
$\displaystyle{x=-1}$のとき$\displaystyle{y=2}$
$\displaystyle{x=1}$のとき$\displaystyle{y=-1}$
となりますので、その情報を先ほどの増減表に加えたいと思います。
また、 $\displaystyle{x=0}$のときの$\displaystyle{y}$の値も求めたいものです。
なぜなら、グラフがy軸のどこで交わっているかを知るためです。
実際、$\displaystyle{x=0}$のとき$\displaystyle{y=0}$であるので、
このグラフの概形を描くときは、原点を通ることを意識して描かなければなりません。
同様に、$\displaystyle{x=0}$のとき$\displaystyle{y}$が正の値であれば、グラフはy軸の正の部分を通るように描かなければなりませんし、
$\displaystyle{y}$が負の値でも同様です。
このようにして、
$\displaystyle{y=x^3-3x}$のグラフの新たな情報を、
以下のように加えました。
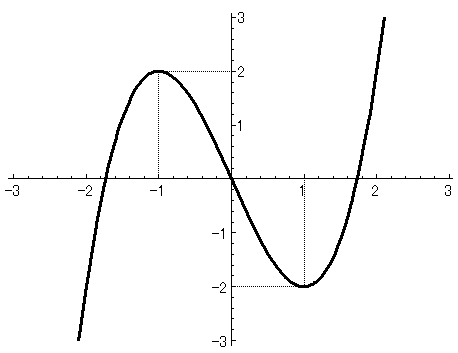
しかし、もう少しだけ正確に描きたいものです。
せめて、
$\displaystyle{x=-1}$と$\displaystyle{x=1}$は、グラフの増減が変わる点でもあるので、
その点での座標を求めたいものです。
この点はもとのグラフ、
$\displaystyle{y=x^3-3x}$に$\displaystyle{x=-1}$と$\displaystyle{x=1}$を代入すれば、すぐに分かります。
代入してみると、
$\displaystyle{x=-1}$のとき$\displaystyle{y=2}$
$\displaystyle{x=1}$のとき$\displaystyle{y=-1}$
となりますので、その情報を先ほどの増減表に加えたいと思います。
| $\displaystyle{x}$ | $\displaystyle{\cdots}$ | $\displaystyle{-1}$ | $\displaystyle{\cdots}$ | $\displaystyle{1}$ | $\displaystyle{\cdots}$ |
|---|---|---|---|---|---|
| $\displaystyle{y'}$ | $\displaystyle{+}$ | $\displaystyle{0}$ | $\displaystyle{-}$ | $\displaystyle{0}$ | $\displaystyle{+}$ |
| $\displaystyle{y}$ | $\displaystyle{\nearrow}$ | $\displaystyle{2}$ | $\displaystyle{\searrow}$ | $\displaystyle{-2}$ | $\displaystyle{\nearrow}$ |
また、 $\displaystyle{x=0}$のときの$\displaystyle{y}$の値も求めたいものです。
なぜなら、グラフがy軸のどこで交わっているかを知るためです。
実際、$\displaystyle{x=0}$のとき$\displaystyle{y=0}$であるので、
このグラフの概形を描くときは、原点を通ることを意識して描かなければなりません。
同様に、$\displaystyle{x=0}$のとき$\displaystyle{y}$が正の値であれば、グラフはy軸の正の部分を通るように描かなければなりませんし、
$\displaystyle{y}$が負の値でも同様です。
このようにして、
$\displaystyle{y=x^3-3x}$のグラフの新たな情報を、
以下のように加えました。