微分とは?
Follow @tepika_math次は点xでの傾きを求めよう
今度は、
$\displaystyle{f(x)=x^3}$上に適当な点$\displaystyle{x}$をとり、その点での接線の傾きを求めたいと思います。
それでわ、いつものように極限値を求めていきましょう。
$\displaystyle{\lim_{h{\rightarrow}0}\frac{(x+h)^3-x^3}h}$
$\displaystyle{\lim_{h{\rightarrow}0}\frac{3x^2h+3xh^2+h^3}h}$
$\displaystyle{\lim_{h{\rightarrow}0}(3x^2+3xh+h^2)}$
$\displaystyle{\lim_{h{\rightarrow}0}3x^2}$
となります。
よって、$\displaystyle{f(x)=x^3}$上の点$\displaystyle{x}$での接線の傾きは、$\displaystyle{3x^2}$となることが分かりました。
ところで、どうでしょう?
もし、この$\displaystyle{3x^2}$に$\displaystyle{x=4}$を代入したら、
$\displaystyle{f(x)}$における$\displaystyle{x=4}$での接線の傾きが求められます。
また同様に、$\displaystyle{3x^2}$に$\displaystyle{x=0}$を代入しても、
同様にしてその地点での接線の傾きが求められます。
ちなみに、この場合x=0を代入してみると0になるので、
この場合、接線の傾きが0ということになります。
こうしてみると、$\displaystyle{3x^2}$というのは、
$\displaystyle{x^3}$のそれぞれの点での接線の傾きを求める
いわば‘公式’みたいなものだと分かっていただけたでしょうか?
このように、関数$\displaystyle{f(x)}$の接線の傾きを求める‘公式’みたいなものを導く操作のことを微分といいます。
また、微分した後の関数のことを導関数といい、
微分する前の関数のことを原始関数といいます。
この場合、$\displaystyle{x^3}$の導関数は$\displaystyle{3x^2}$となり、
逆に、$\displaystyle{3x^2}$の原始関数は$\displaystyle{x^3}$となります。
以下に$\displaystyle{f(x)=x^3}$のグラフを示します。
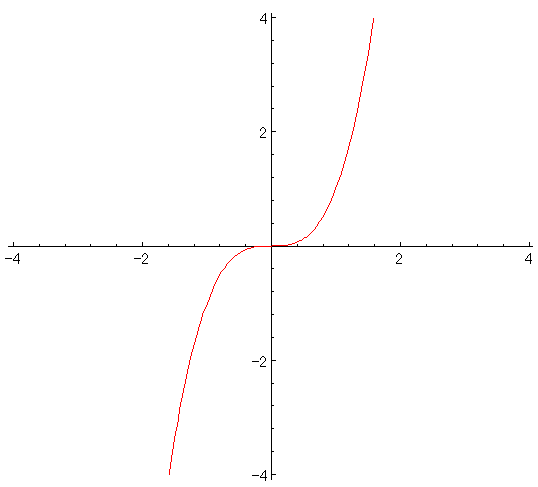
$\displaystyle{x^3}$の導関数$\displaystyle{3x^2}$は、x=0の時最小値0をとり、それ以外は、必ず正の値をとります。
よって、もとの関数$\displaystyle{f(x)=x^3}$は、x=0以外の全ての点で接線の傾きが正、つまり右上がりになります。
また、x=0の点では、接線の傾きが0となるため、グラフの増加がいったん緩やかになっています。
$\displaystyle{f(x)=x^3}$上に適当な点$\displaystyle{x}$をとり、その点での接線の傾きを求めたいと思います。
それでわ、いつものように極限値を求めていきましょう。
$\displaystyle{\lim_{h{\rightarrow}0}\frac{(x+h)^3-x^3}h}$
$\displaystyle{\lim_{h{\rightarrow}0}\frac{3x^2h+3xh^2+h^3}h}$
$\displaystyle{\lim_{h{\rightarrow}0}(3x^2+3xh+h^2)}$
$\displaystyle{\lim_{h{\rightarrow}0}3x^2}$
となります。
よって、$\displaystyle{f(x)=x^3}$上の点$\displaystyle{x}$での接線の傾きは、$\displaystyle{3x^2}$となることが分かりました。
ところで、どうでしょう?
もし、この$\displaystyle{3x^2}$に$\displaystyle{x=4}$を代入したら、
$\displaystyle{f(x)}$における$\displaystyle{x=4}$での接線の傾きが求められます。
また同様に、$\displaystyle{3x^2}$に$\displaystyle{x=0}$を代入しても、
同様にしてその地点での接線の傾きが求められます。
ちなみに、この場合x=0を代入してみると0になるので、
この場合、接線の傾きが0ということになります。
こうしてみると、$\displaystyle{3x^2}$というのは、
$\displaystyle{x^3}$のそれぞれの点での接線の傾きを求める
いわば‘公式’みたいなものだと分かっていただけたでしょうか?
このように、関数$\displaystyle{f(x)}$の接線の傾きを求める‘公式’みたいなものを導く操作のことを微分といいます。
また、微分した後の関数のことを導関数といい、
微分する前の関数のことを原始関数といいます。
この場合、$\displaystyle{x^3}$の導関数は$\displaystyle{3x^2}$となり、
逆に、$\displaystyle{3x^2}$の原始関数は$\displaystyle{x^3}$となります。
以下に$\displaystyle{f(x)=x^3}$のグラフを示します。
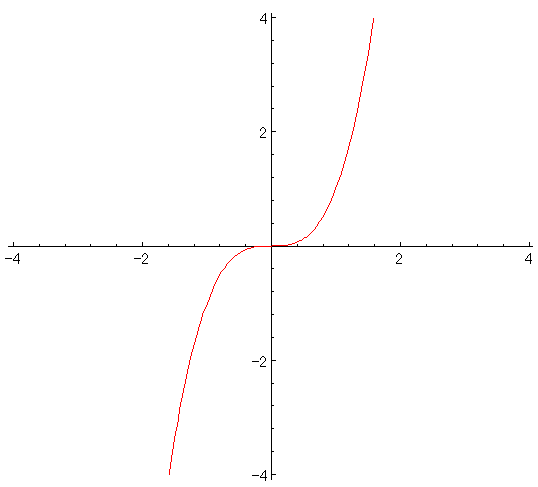
$\displaystyle{x^3}$の導関数$\displaystyle{3x^2}$は、x=0の時最小値0をとり、それ以外は、必ず正の値をとります。
よって、もとの関数$\displaystyle{f(x)=x^3}$は、x=0以外の全ての点で接線の傾きが正、つまり右上がりになります。
また、x=0の点では、接線の傾きが0となるため、グラフの増加がいったん緩やかになっています。
導関数の表し方
それでは、おさらいしましょう。
このように、関数$\displaystyle{f(x)}$の導関数は、
$\displaystyle{\lim_{h{\rightarrow}0}\frac{f(x+h)-f(x)}h}$のように求められます。
また、$\displaystyle{f(x)}$の導関数は、
$\displaystyle{f'(x)}$や$\displaystyle{\dot{f}(x)}$
あるいは、
$\displaystyle{\frac{df(x)}{dx}}$や$\displaystyle{\frac{d}{dx}f(x)}$と表されます。
「なぜ導関数の表し方がいくつかもあるの?」と思うかもしれませんが、
それは「微分」を発見した人物が二人いるからです。
どういうことかといいますと、偶然にも二人同時に微分を発見してしまったのです。
その二人の人物は、あの「木から落ちるリンゴ」で有名なニュートンと、
数学者の「ライプニッツ」だと言われています。
だから現在でも、「一体どっちが微分を発見したんだ?」なんて論争が絶えませんが・・・
ニュートンは導関数を$\displaystyle{\dot{f}(x)}$で表しました。 またライプニッツは導関数を$\displaystyle{\frac{df(x)}{dx}}$や$\displaystyle{\frac{d}{dx}f(x)}$で表しました。
このように、二人の人物が独立で微分を発見したため、記法も幾通りになってしまったということです。
ちなみに、$\displaystyle{f'(x)}$は、ラグランジュという人が考案した記法です。
ところで、ライプニッツの記法に出てくる$\displaystyle{d}$ですが、これは数ではなくて記号です。
この$\displaystyle{d}$は、今までの$\displaystyle{x}$や$\displaystyle{a}$のように数を文字で割り当てたものではなく、
総和を求める$\displaystyle{\sum}$みたいな、記号だと思ってください。
このように、関数$\displaystyle{f(x)}$の導関数は、
$\displaystyle{\lim_{h{\rightarrow}0}\frac{f(x+h)-f(x)}h}$のように求められます。
また、$\displaystyle{f(x)}$の導関数は、
$\displaystyle{f'(x)}$や$\displaystyle{\dot{f}(x)}$
あるいは、
$\displaystyle{\frac{df(x)}{dx}}$や$\displaystyle{\frac{d}{dx}f(x)}$と表されます。
「なぜ導関数の表し方がいくつかもあるの?」と思うかもしれませんが、
それは「微分」を発見した人物が二人いるからです。
どういうことかといいますと、偶然にも二人同時に微分を発見してしまったのです。
その二人の人物は、あの「木から落ちるリンゴ」で有名なニュートンと、
数学者の「ライプニッツ」だと言われています。
だから現在でも、「一体どっちが微分を発見したんだ?」なんて論争が絶えませんが・・・
ニュートンは導関数を$\displaystyle{\dot{f}(x)}$で表しました。 またライプニッツは導関数を$\displaystyle{\frac{df(x)}{dx}}$や$\displaystyle{\frac{d}{dx}f(x)}$で表しました。
このように、二人の人物が独立で微分を発見したため、記法も幾通りになってしまったということです。
ちなみに、$\displaystyle{f'(x)}$は、ラグランジュという人が考案した記法です。
ところで、ライプニッツの記法に出てくる$\displaystyle{d}$ですが、これは数ではなくて記号です。
この$\displaystyle{d}$は、今までの$\displaystyle{x}$や$\displaystyle{a}$のように数を文字で割り当てたものではなく、
総和を求める$\displaystyle{\sum}$みたいな、記号だと思ってください。