積分とは、微分の逆のことです。



原始関数から、導関数を導く過程を微分というのでした。

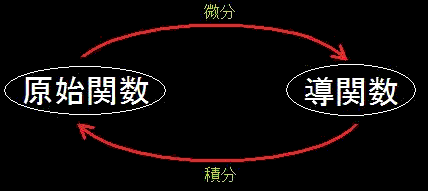
上の図のように、導関数から原始関数に戻すことを「積分」というのです。

だから、
$\displaystyle{x^2}$を微分したら$\displaystyle{2x}$になるので、
$\displaystyle{2x}$を積分したら$\displaystyle{x^2}$になります。

ほらね？簡単でしょ☆~

それじゃあ、$\displaystyle{x^2}$の積分は？？
一体、何を微分したら$\displaystyle{x^2}$になるでしょうか？
$\displaystyle{\frac13x^3}$のようですね。
・・・というように、積分を見つけるだけでも、ひとくろう〜ε(-o-)

例えば、$\displaystyle{x^2}$の積分は以下のように書かれます。
$\displaystyle{\int{x^2dx}}$
なんだか、微分よりも積分の記号の方が、かっこいい(？)ですね〜。。。

だから、
$\displaystyle{\int{x^2dx}=\frac13x^3}$
となります。


ところで、後ろのｄｘって何だ？？？と思うかもしれません。
このｄは数ではありません。記号です。

つまりこのｄは、今までのｘ，ｙやａ，ｂ，ｃのような、数を文字に置き換えたものではなく、
総和を表すΣや三角関数のｓｉｎのような、いわゆる記号の一種であり、
どの変数で積分するか、というのを表しています。
たとえば、ｄｘでしたら「ｘで積分する」という意味ですし、
もしｄａになっていたら、「変数ａで積分しなさい」という意味になります。

だから、もし
$\displaystyle{\int{2axda}}$
となっていた場合、これはａで積分されます。
もちろんｘは関係ないので、
$\displaystyle{\int{2axda=a^2x}}$
となります。
この原始関数をａで微分したら、ちゃんと２ａｘになってくれるのが分かると思います。

ところで、本当に
$\displaystyle{2x}$を積分したら$\displaystyle{x^2}$ですっ！！！と答えてしまわないように。。。
まぁこれでも間違いではないですが、△(さんかく)ってとこですかねぇ・・・


どういうことかと言いますと・・・
確かに$\displaystyle{x^2}$を微分したらちゃんと$\displaystyle{2x}$になるのですが・・・
よく考えてみると
$\displaystyle{x^2+1}$を微分しても、$\displaystyle{2x}$になるし、
$\displaystyle{x^2+2}$を微分しても、$\displaystyle{2x}$になります。
当然のように、$\displaystyle{x^2+3}$も$\displaystyle{x^2+4}$も 微分したら$\displaystyle{2x}$になることを考えると、
原始関数はいくらでも作れることになります。
そう、原始関数は無限個あることになります！！！
困りましたネェ・・・(´;ω;｀)

この場合、まぁとりあえず、２ｘの積分は、
$\displaystyle{\int{2xdx}=x^2+C}$
みたいに、適当な文字$\displaystyle{C}$と置いてしまいます。
この$\displaystyle{C}$を、積分定数と呼びます。