三角形の回転
Follow @tepika_math数以外の群って?
数の集合じゃなくても、群になることができると、以前説明しました。
しかし、数以外に二項演算子を定義する・・・なぁんて言われても、
何だかあまりぱっとしませんねぇ〜。
そこで、群の例を用意しました。
しかし、数以外に二項演算子を定義する・・・なぁんて言われても、
何だかあまりぱっとしませんねぇ〜。
そこで、群の例を用意しました。
三角形の回転の操作
例えば、以下のような三角形を考えましょう。
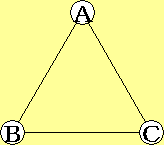
この三角形を、右に120度回転させる操作を、文字$\displaystyle{r}$で表すとします。
同様に、 この三角形を、左に120度回転させる操作を、文字$\displaystyle{l}$で表すとします。
つまり、こういうことです。
120度回転してるので、各頂点、A,B,Cが入れ替わっているのが分かります。
今度は、以下の図のように、縦軸をa軸、
右上がりの軸をb軸
右下がりの軸をcとして、
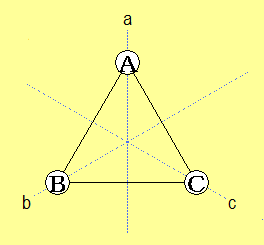
a軸を中心として裏返す操作を$\displaystyle{a}$
b軸を中心として裏返す操作を$\displaystyle{b}$
c軸を中心として裏返す操作を$\displaystyle{c}$
とします。
操作$\displaystyle{a}$と$\displaystyle{b}$と$\displaystyle{c}$は、以下のようになります。
また、三角形を回転させない、つまりなにも動かさない操作もかんがえましょう。
それを$\displaystyle{e}$としましょう。
この三角形に$\displaystyle{e}$を操作させても、何も変化がありません。
つまり、$\displaystyle{e}$とは、無意味な操作です。
「なぜこの操作を考えるの?」・・・それは後ほど説明いたします。。。
これで、この三角形に $\displaystyle{e,r,l,a,b,c}$と、6つの操作を定義しました。

この三角形を、右に120度回転させる操作を、文字$\displaystyle{r}$で表すとします。
同様に、 この三角形を、左に120度回転させる操作を、文字$\displaystyle{l}$で表すとします。
つまり、こういうことです。
 |
$\displaystyle{r}$ → |
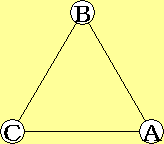 |
| $\displaystyle{l}$ → |
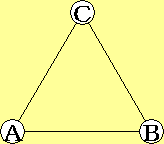 |
今度は、以下の図のように、縦軸をa軸、
右上がりの軸をb軸
右下がりの軸をcとして、

a軸を中心として裏返す操作を$\displaystyle{a}$
b軸を中心として裏返す操作を$\displaystyle{b}$
c軸を中心として裏返す操作を$\displaystyle{c}$
とします。
操作$\displaystyle{a}$と$\displaystyle{b}$と$\displaystyle{c}$は、以下のようになります。
 |
$\displaystyle{a}$ → |
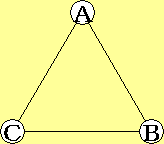 |
| $\displaystyle{b}$ → |
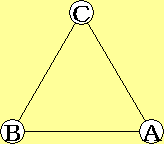 |
|
| $\displaystyle{c}$ → |
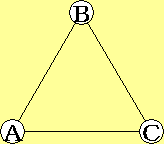 |
それを$\displaystyle{e}$としましょう。
この三角形に$\displaystyle{e}$を操作させても、何も変化がありません。
つまり、$\displaystyle{e}$とは、無意味な操作です。
「なぜこの操作を考えるの?」・・・それは後ほど説明いたします。。。
これで、この三角形に $\displaystyle{e,r,l,a,b,c}$と、6つの操作を定義しました。
各操作の演算
この6つの、$\displaystyle{e,r,l,a,b,c}$に、演算子を定義します。
例えば、 $\displaystyle{ar}$を、三角形に「操作$\displaystyle{r}$をしてから、操作$\displaystyle{a}$をする」操作というように定義しましょう。
つまり、三角形に操作$\displaystyle{ar}$をしたら、
となります。
気をつけるべき点としては、文字$\displaystyle{a}$が先にきますが、
でも、操作$\displaystyle{a}$をするのは後です。
後ろの文字から操作する、とうように演算子を定義したことに気をつけてください。
ところで、この三角形に操作$\displaystyle{c}$をしても、
となってしまいます。
なんと操作$\displaystyle{ar}$と操作$\displaystyle{c}$とは、結果が一緒なのです。
だから、操作$\displaystyle{ar}$と操作$\displaystyle{c}$は、同じことをやっている、と見なすことはできないでしょうか?
こうして
$\displaystyle{ar=c}$
という等式が成り立ちます。
このように、各操作に対してこのような演算をすると、以下のような表になります。
こうしてみると、これって何だか「群」になりそうですよね?
この6つの操作は、この演算子に閉じています。
結合律は・・・自分で確かめてみてください。きっと成り立ちます!!!
この演算子には、何も操作しない$\displaystyle{e}$という操作が存在します。
また、各操作にはそれぞれ逆元が存在していそうです。
これで、群の4つの性質が全てそろいました。
つまり、三角形を回転する「操作」自体にも、このように演算子を定義すれば、群になることができるのです。
しかし見て分かる通り、この群は可換ではないようです。
例えば、 $\displaystyle{ar}$を、三角形に「操作$\displaystyle{r}$をしてから、操作$\displaystyle{a}$をする」操作というように定義しましょう。
つまり、三角形に操作$\displaystyle{ar}$をしたら、
 |
$\displaystyle{r}$ → |
 |
$\displaystyle{a}$ → |
 |
気をつけるべき点としては、文字$\displaystyle{a}$が先にきますが、
でも、操作$\displaystyle{a}$をするのは後です。
後ろの文字から操作する、とうように演算子を定義したことに気をつけてください。
ところで、この三角形に操作$\displaystyle{c}$をしても、
 |
$\displaystyle{c}$ → |
 |
なんと操作$\displaystyle{ar}$と操作$\displaystyle{c}$とは、結果が一緒なのです。
だから、操作$\displaystyle{ar}$と操作$\displaystyle{c}$は、同じことをやっている、と見なすことはできないでしょうか?
こうして
$\displaystyle{ar=c}$
という等式が成り立ちます。
このように、各操作に対してこのような演算をすると、以下のような表になります。
| $\displaystyle{e}$ | $\displaystyle{r}$ | $\displaystyle{l}$ | $\displaystyle{a}$ | $\displaystyle{b}$ | $\displaystyle{c}$ | ||
|---|---|---|---|---|---|---|---|
| $\displaystyle{e}$ | $\displaystyle{e}$ | $\displaystyle{r}$ | $\displaystyle{l}$ | $\displaystyle{a}$ | $\displaystyle{b}$ | $\displaystyle{c}$ | |
| $\displaystyle{r}$ | $\displaystyle{r}$ | $\displaystyle{l}$ | $\displaystyle{e}$ | $\displaystyle{b}$ | $\displaystyle{c}$ | $\displaystyle{a}$ | |
| $\displaystyle{l}$ | $\displaystyle{l}$ | $\displaystyle{e}$ | $\displaystyle{r}$ | $\displaystyle{c}$ | $\displaystyle{a}$ | $\displaystyle{b}$ | |
| $\displaystyle{a}$ | $\displaystyle{a}$ | $\displaystyle{c}$ | $\displaystyle{b}$ | $\displaystyle{e}$ | $\displaystyle{l}$ | $\displaystyle{r}$ | |
| $\displaystyle{b}$ | $\displaystyle{b}$ | $\displaystyle{a}$ | $\displaystyle{c}$ | $\displaystyle{r}$ | $\displaystyle{e}$ | $\displaystyle{l}$ | |
| $\displaystyle{c}$ | $\displaystyle{c}$ | $\displaystyle{b}$ | $\displaystyle{a}$ | $\displaystyle{l}$ | $\displaystyle{r}$ | $\displaystyle{e}$ |
この6つの操作は、この演算子に閉じています。
結合律は・・・自分で確かめてみてください。きっと成り立ちます!!!
この演算子には、何も操作しない$\displaystyle{e}$という操作が存在します。
また、各操作にはそれぞれ逆元が存在していそうです。
これで、群の4つの性質が全てそろいました。
つまり、三角形を回転する「操作」自体にも、このように演算子を定義すれば、群になることができるのです。
しかし見て分かる通り、この群は可換ではないようです。
まとめ
このように、群は何も数だけじゃないことが分かって頂けたでしょうか?
群の性質を満たすような演算子を定義することができたら、なんでも群になることができます。
また演算子も、従来の掛け算や足し算とは全然違ったものでも、それが群の性質を満たすようなものであれば、何でも群です。
以上の例は三角形の回転を群として扱いましたが、
化学の世界では、分子の回転などを群で扱うことがあるそうです。
群の性質を満たすような演算子を定義することができたら、なんでも群になることができます。
また演算子も、従来の掛け算や足し算とは全然違ったものでも、それが群の性質を満たすようなものであれば、何でも群です。
以上の例は三角形の回転を群として扱いましたが、
化学の世界では、分子の回転などを群で扱うことがあるそうです。