線形空間が基底をもつとき、その基底のベクトルの個数のことを、その線形空間の次元と言います。


線形空間$\displaystyle{V}$の次元は
$\displaystyle{\mathrm{dim}V}$
と表されます。



例えば$\displaystyle{V}$の基底が$\displaystyle{v_1,v_2,\cdots,v_n}$のとき、
線形空間$\displaystyle{V}$の次元は$\displaystyle{n}$であり、
$\displaystyle{\mathrm{dim}V=n}$
です。

上の青色の領域(ていぅか、平面全体)は、線形空間でした。

$\displaystyle{u_1=\begin{pmatrix}1\\0\end{pmatrix}}$
$\displaystyle{u_1=\begin{pmatrix}0\\1\end{pmatrix}}$
として、上の図の青色の領域は$\displaystyle{u_1,u_2}$と２つのベクトルを基底とした線形空間と考えられます。
よって上の青色の領域の次元は２ですね！！

次に、以下のものを考えましょう。

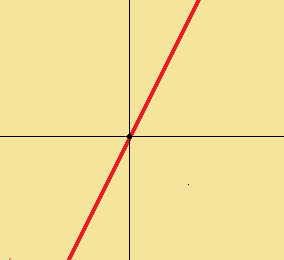
赤色の直線は$\displaystyle{y=2x}$のグラフ、つまり傾きが２の比例のグラフです。

また２成分のベクトルで$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で$\displaystyle{2x-y=0}$を満たすもの全体からなるものだと考えてもいいです。
この赤色の直線も線形空間を成しています。


この赤色の直線で表された線形空間を$\displaystyle{V}$としますと、
$\displaystyle{V}$の基底は
$\displaystyle{\begin{pmatrix}1\\2\end{pmatrix}}$
と、１つのベクトルになります。


$\displaystyle{V}$に属する任意のベクトルは
$\displaystyle{t\begin{pmatrix}1\\2\end{pmatrix}=\begin{pmatrix}t\\2t\end{pmatrix}}$
と、$\displaystyle{t}$を適当に選ぶことによって得られます。

なので、この線形空間$\displaystyle{V}$の次元は１ですね！！



気をつけるべき点として、$\displaystyle{V}$に属するベクトルは２成分(２次元ベクトル)であるにも関わらず、
線形空間$\displaystyle{V}$の次元は１ということに気をつけて下さい☆