線形空間の例
Follow @tepika_mathまずは直線の例で
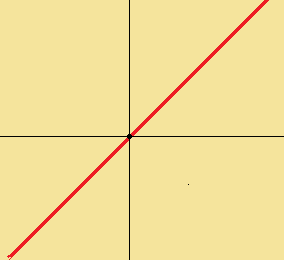
この赤色の直線は、線形空間になります。
ちなみに、この直線は関数$\displaystyle{y=x}$の、傾きが1の比例のグラフのつもりで描きました(・・;
この直線は無限の彼方まで伸びていると仮定しています。
もちろん、途中で途切れている直線(線分とか)は、線形空間になりませんね。
線形空間の定義として、
- $\displaystyle{0 \in V}$である。ここで$\displaystyle{0}$はゼロベクトルである
- $\displaystyle{v_1,v_2 \in V}$ならば$\displaystyle{v_1+v_2 \in V}$
- $\displaystyle{v \in V}$ならば、任意の実数$\displaystyle{c}$に対して$\displaystyle{cv \in V}$
この直線は、明らかに原点を通っていますので、条件1.は満たしております。
条件2.や3.も同様に満たしていますよね?
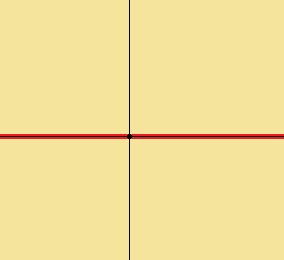
これは分かりますか?
これはx軸上に重なっている赤い直線ですね。
この直線を$\displaystyle{L}$としますと、
$\displaystyle{\begin{pmatrix}0\\0\end{pmatrix} \in L}$
$\displaystyle{\begin{pmatrix}3\\0\end{pmatrix} \in L}$
$\displaystyle{\begin{pmatrix}{-1}\\0\end{pmatrix} \in L}$
・
・
・
となります。
この直線は、線形空間の条件を満たしているので(自分で確かめてみましょう)、これは線形空間です。
線形空間ではない直線
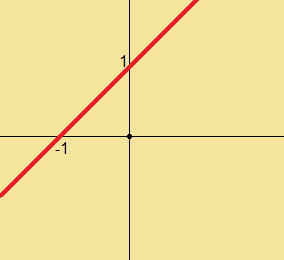
この直線を見て下さい。
これは線形空間ではないです。
これは$\displaystyle{y=x+1}$と、傾きが1で切片が1の一次関数のグラフを表現してみましたm(_ _)m
例えば、この直線を$\displaystyle{L}$としますと、
$\displaystyle{\begin{pmatrix}{-2}\\{-1}\end{pmatrix} \in L}$
$\displaystyle{\begin{pmatrix}{-1}\\0\end{pmatrix} \in L}$
$\displaystyle{\begin{pmatrix}0\\1\end{pmatrix} \in L}$
$\displaystyle{\begin{pmatrix}3\\4\end{pmatrix} \in L}$
・
・
・
ということが分かるでしょうか?
この直線には、まず原点が含まれていません。
よって線形空間の条件1.を満たしていないのです。
その時点で、この直線はダメですね・・・

実は、このクロスした2本の直線、これも線形空間ではないのです。
この2本の直線を$\displaystyle{L}$としましょう。
確かに$\displaystyle{L}$は原点を通ります。
よって、条件1.を満たしていますね。
また、条件3.を満たしていることも確かめられます。
しかし条件2.が満たされていないのです!!!
条件2.をもう一度振り返ってみると、
「ベクトルuとvが線形空間の元ならば、その和u+vも線形空間の元である」
でした!!
まず、
$\displaystyle{u=\begin{pmatrix}1\\0\end{pmatrix} \quad v=\begin{pmatrix}0\\1\end{pmatrix}}$
としましょう。
そうすると
$\displaystyle{u \in L \quad v \in L}$
となることが分かります。
ところで
$\displaystyle{u + v = \begin{pmatrix}1\\1\end{pmatrix}}$
となります。
当然
$\displaystyle{\begin{pmatrix}1\\1\end{pmatrix} \notin L}$
であるので、
$\displaystyle{u+v \notin L}$
となってしまいます。
条件2.を言い換えますと、
「どんな線形空間の元$\displaystyle{u,v}$に対しても、その元の和$\displaystyle{u+v}$も線形空間の元である」
ということなので、よって条件2に例外が出てしまったことが明らかだと思います。
線形空間でない例
逆に↓は線形空間ではありません。
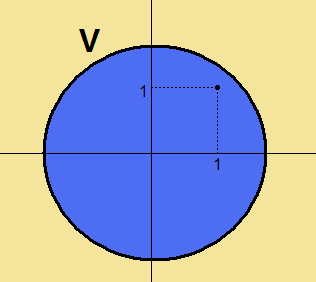
上の図で青色に描かれた領域を$\displaystyle{V}$としましょう。
上の青い領域は、線形空間の条件3.である
「$\displaystyle{v_1,v_2 \in V}$ならば$\displaystyle{v_1+v_2 \in V}$」
を満たしておりません。
さて、下の図は、上の図に矢印を加えただけの図です。
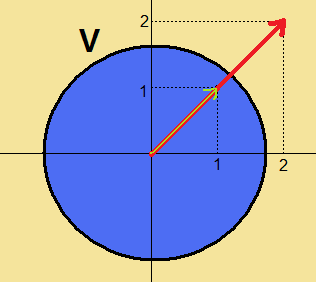
緑色のベクトルである$\displaystyle{\begin{pmatrix}1\\1\end{pmatrix}}$は、領域$\displaystyle{V}$に含まれていることが分かります。
つまり、
$\displaystyle{\begin{pmatrix}1\\1\end{pmatrix} \in V}$
です。
一方、線形空間の条件3として$\displaystyle{u}$がベクトル空間の元ならその定数倍である$\displaystyle{cu}$もベクトル空間に含まれなければならない」という条件があります。
図の赤色のベクトルは、緑色のベクトルの2倍の長さを持っています。
赤色のベクトルは緑色のベクトルの定数倍なのです。
それにもかかわらず、緑色のベクトルは青色の領域の中に含まれていませんよね?
同様に↓の青い領域も線形空間ではありません。
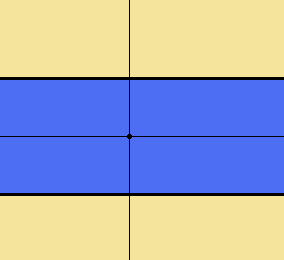
そう考えますと、有限(有界?)な領域は線形空間にはなりそうもないですね・・・

上の図で青色に描かれた領域を$\displaystyle{V}$としましょう。
上の青い領域は、線形空間の条件3.である
「$\displaystyle{v_1,v_2 \in V}$ならば$\displaystyle{v_1+v_2 \in V}$」
を満たしておりません。
さて、下の図は、上の図に矢印を加えただけの図です。

緑色のベクトルである$\displaystyle{\begin{pmatrix}1\\1\end{pmatrix}}$は、領域$\displaystyle{V}$に含まれていることが分かります。
つまり、
$\displaystyle{\begin{pmatrix}1\\1\end{pmatrix} \in V}$
です。
一方、線形空間の条件3として$\displaystyle{u}$がベクトル空間の元ならその定数倍である$\displaystyle{cu}$もベクトル空間に含まれなければならない」という条件があります。
図の赤色のベクトルは、緑色のベクトルの2倍の長さを持っています。
赤色のベクトルは緑色のベクトルの定数倍なのです。
それにもかかわらず、緑色のベクトルは青色の領域の中に含まれていませんよね?
同様に↓の青い領域も線形空間ではありません。

そう考えますと、有限(有界?)な領域は線形空間にはなりそうもないですね・・・
