領域と集合
Follow @tepika_math空間内の領域
はい!
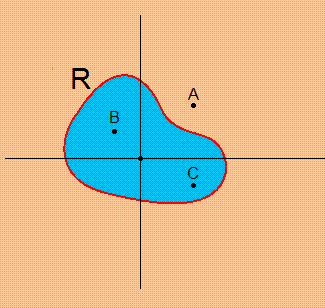
上の図で青色に塗られた領域をRとしましょう。
ここで、点A,B,Cの座標をそれぞれ
$\displaystyle{A=(1,1)}$
$\displaystyle{B=(-1/2, 1/2)}$
$\displaystyle{C=(1,-1/2)}$
とします。
さてさて、“領域”と言ったら、「空間の一部分」と考えるのが普通ですが、
少し視点を変えますと領域というのは実は「無数の点の集まり」なんだよ!とも考えられないでしょうか?
「無数の点が集まって、一つの領域を形成している・・・!」
最初にこの言葉を聞いた時、きっとビックリするのではないでしょうか?(←そうでもないカナ?)
例えば領域Rを、本当に点の集まりだとしますと、
領域Rの中には点Aは含まれていませんが、点Bと点Cは領域Rの中に含まれています。
こうして、Rとは点を元としてもつ集合と考えます。
(集合論の一般論はコチラを参照してください)
そう考えると「領域というのは滅茶苦茶な数の点の集まりなんだな・・・」というのが分かると思います。
ベクトルの集合?
さて、以前
「座標とベクトルを同一視する」
ということをお話しました。
このようなベクトルのことを位置ベクトルといいます。
つまり
$\displaystyle{\begin{pmatrix}1\\1\\\end{pmatrix}}$
$\displaystyle{\begin{pmatrix}-1/2\\1/2\end{pmatrix}}$
$\displaystyle{\begin{pmatrix}1\\-1/2\end{pmatrix}}$
とすると以下の図のようになります。
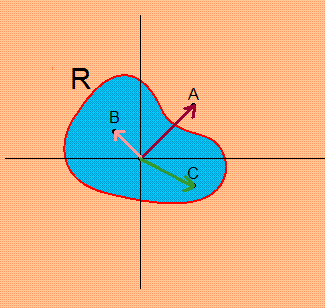
この場合$\displaystyle{v_A,v_B,v_C}$がそれぞれ赤のベクトル、ピンクのベクトル、緑のベクトルに対応します。
つまり領域とは
「無数の点の集合」とも「無数のベクトルの集合」とも考えられます。
「座標とベクトルを同一視する」
ということをお話しました。
このようなベクトルのことを位置ベクトルといいます。
つまり
$\displaystyle{\begin{pmatrix}1\\1\\\end{pmatrix}}$
$\displaystyle{\begin{pmatrix}-1/2\\1/2\end{pmatrix}}$
$\displaystyle{\begin{pmatrix}1\\-1/2\end{pmatrix}}$
とすると以下の図のようになります。

この場合$\displaystyle{v_A,v_B,v_C}$がそれぞれ赤のベクトル、ピンクのベクトル、緑のベクトルに対応します。
つまり領域とは
「無数の点の集合」とも「無数のベクトルの集合」とも考えられます。
集合の包含関係
「ベクトルの集合」という概念は分かりましたか?
$\displaystyle{V}$をベクトルの集合とします。
このとき、ベクトル$\displaystyle{v}$が$\displaystyle{V}$の中にあるとき、
$\displaystyle{v{\in}V}$
と表します。
そして$\displaystyle{v}$は集合$\displaystyle{V}$の元であるといいます。
例えば

で、上の青色の領域を$\displaystyle{R}$としたとき、
$\displaystyle{v_A{\notin}R}$
$\displaystyle{v_B{\in}R}$
$\displaystyle{v_C{\in}R}$
となります。 $\displaystyle{v_B,v_C}$は集合$\displaystyle{R}$の元ですが、
$\displaystyle{v_A}$は集合$\displaystyle{R}$の元ではありません。
$\displaystyle{V}$をベクトルの集合とします。
このとき、ベクトル$\displaystyle{v}$が$\displaystyle{V}$の中にあるとき、
$\displaystyle{v{\in}V}$
と表します。
そして$\displaystyle{v}$は集合$\displaystyle{V}$の元であるといいます。
例えば

で、上の青色の領域を$\displaystyle{R}$としたとき、
$\displaystyle{v_A{\notin}R}$
$\displaystyle{v_B{\in}R}$
$\displaystyle{v_C{\in}R}$
となります。 $\displaystyle{v_B,v_C}$は集合$\displaystyle{R}$の元ですが、
$\displaystyle{v_A}$は集合$\displaystyle{R}$の元ではありません。
直線
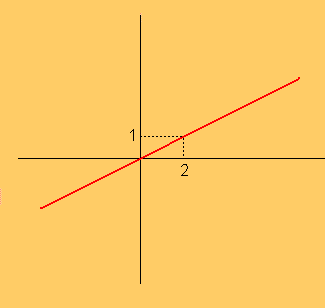
はい、上の赤色の直線を考えます。
直線は「空間の一部分」であるので、
一応、直線も“領域”と考えられますね。
つまり、直線自体も「点の集まり」あるいは「無数のベクトルの集まり」と考えられます。
上の赤色の直線を$\displaystyle{l}$とます。
そして、 直線$\displaystyle{l}$のグラフの式を $\displaystyle{y=\frac{1}{2}x}$としますと、
座標$\displaystyle{(0,0), (4,2), (-2,-1)}$も、直線$\displaystyle{l}$上の点ですので、
集合の記号を使って表しますと、
$\displaystyle{\begin{pmatrix}0\\0\\ \end{pmatrix}{\in}l}$
$\displaystyle{\begin{pmatrix}4\\2\\ \end{pmatrix}{\in}l}$
$\displaystyle{\begin{pmatrix}{-2}\\{-1}\\ \end{pmatrix}{\in}l}$
となります。
直線と平面と空間
$\displaystyle{\mathbb{R}^2}$を、2成分のベクトルを全て集めた集合とします。
例えば、どんな$\displaystyle{a,b}$に対しても
$\displaystyle{\begin{pmatrix}a\\b\\ \end{pmatrix}\in\mathbb{R}^2}$ が成り立ちますよね?
また、$\displaystyle{\mathbb{R}^2}$は、2次元平面の全体の領域だということが分かるでしょうか?
同様に$\displaystyle{\mathbb{R}^3}$を3成分のベクトルを全て集めた集合と考えますと、
$\displaystyle{\mathbb{R}^3}$というのは、3次元空間の全体の領域になります。
例えば、どんな$\displaystyle{a,b}$に対しても
$\displaystyle{\begin{pmatrix}a\\b\\ \end{pmatrix}\in\mathbb{R}^2}$ が成り立ちますよね?
また、$\displaystyle{\mathbb{R}^2}$は、2次元平面の全体の領域だということが分かるでしょうか?
同様に$\displaystyle{\mathbb{R}^3}$を3成分のベクトルを全て集めた集合と考えますと、
$\displaystyle{\mathbb{R}^3}$というのは、3次元空間の全体の領域になります。