線形部分空間
Follow @tepika_math空間の一部
下の図を見て下さい。
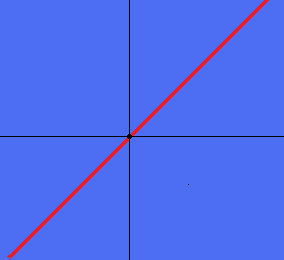
この、青色で描かれた領域(つまり平面全体です)を$\displaystyle{\mathbb{R}^2}$とします。
この$\displaystyle{\mathbb{R}^2}$が線形空間になることは以前やりましたよね?
ところで、この図の中に赤色の直線がありますよね?
この赤色の部分(直線)も実は線形空間を成しています。
その赤色の線で描かれた線形空間を$\displaystyle{V}$とします。
見て分かる通り、
上の赤色の線$\displaystyle{V}$は領域$\displaystyle{\mathbb{R}^2}$の一部分であることが分かりますか?
(↑集合論的な書き方では、この事実を$\displaystyle{\mathbb{R}^2 \subset V}$と表します。ここで$\displaystyle{\subset}$は部分集合を表す記号です)
さて、もう一度繰り返しますと↓
$\displaystyle{\mathbb{R}^2}$は線形空間を成しています。
一方、$\displaystyle{\mathbb{R}^2}$の一部である$\displaystyle{V}$自身も、また同じようにして線形空間を成していますね。
このように$\displaystyle{W}$を線形空間として、
その一部$\displaystyle{V}$もまた線形空間を成しているとき、
$\displaystyle{V}$を$\displaystyle{W}$の部分線形空間と言います。
例えば、上の例で言えば、
赤色の直線$\displaystyle{V}$は線形空間でもあり、 また$\displaystyle{\mathbb{R}^2}$の一部でもあります。
そして$\displaystyle{\mathbb{R}^2}$自身も線形空間であるので、
$\displaystyle{V}$は$\displaystyle{\mathbb{R}^2}$の部分線形空間と言えます。

この、青色で描かれた領域(つまり平面全体です)を$\displaystyle{\mathbb{R}^2}$とします。
この$\displaystyle{\mathbb{R}^2}$が線形空間になることは以前やりましたよね?
ところで、この図の中に赤色の直線がありますよね?
この赤色の部分(直線)も実は線形空間を成しています。
その赤色の線で描かれた線形空間を$\displaystyle{V}$とします。
見て分かる通り、
上の赤色の線$\displaystyle{V}$は領域$\displaystyle{\mathbb{R}^2}$の一部分であることが分かりますか?
(↑集合論的な書き方では、この事実を$\displaystyle{\mathbb{R}^2 \subset V}$と表します。ここで$\displaystyle{\subset}$は部分集合を表す記号です)
さて、もう一度繰り返しますと↓
$\displaystyle{\mathbb{R}^2}$は線形空間を成しています。
一方、$\displaystyle{\mathbb{R}^2}$の一部である$\displaystyle{V}$自身も、また同じようにして線形空間を成していますね。
このように$\displaystyle{W}$を線形空間として、
その一部$\displaystyle{V}$もまた線形空間を成しているとき、
$\displaystyle{V}$を$\displaystyle{W}$の部分線形空間と言います。
例えば、上の例で言えば、
赤色の直線$\displaystyle{V}$は線形空間でもあり、 また$\displaystyle{\mathbb{R}^2}$の一部でもあります。
そして$\displaystyle{\mathbb{R}^2}$自身も線形空間であるので、
$\displaystyle{V}$は$\displaystyle{\mathbb{R}^2}$の部分線形空間と言えます。
部分線形空間の定義
もう一度、部分線形空間の定義をまとめます。
$\displaystyle{U}$を線形空間とする。
$\displaystyle{V}$が$\displaystyle{U}$の一部分であって
(↑↑正確に言えば、$\displaystyle{V}$が$\displaystyle{U}$の部分集合、つまり$\displaystyle{V \subset U}$であるとき)
かつ$\displaystyle{V}$もまた線形空間を成しているとき、
$\displaystyle{V}$を$\displaystyle{U}$の部分線形空間と言います。
$\displaystyle{U}$を線形空間とする。
$\displaystyle{V}$が$\displaystyle{U}$の一部分であって
(↑↑正確に言えば、$\displaystyle{V}$が$\displaystyle{U}$の部分集合、つまり$\displaystyle{V \subset U}$であるとき)
かつ$\displaystyle{V}$もまた線形空間を成しているとき、
$\displaystyle{V}$を$\displaystyle{U}$の部分線形空間と言います。
例
次の3つの例のうち、$\displaystyle{\mathbb{R}^2}$の部分線形空間となるものが、1つだけあります。
1.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{xy \geqq 0}$を満たすもの全体
2.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{y=0}$でないもの全体
3.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{x+y=0}$を満たすもの全体
1.の領域は、下の図で青色に塗られた領域を表しています(黒線の領域も含める)。

2.の領域は、下の図で青色に塗られた領域を表しています。つまりx軸だけ取り除いた空間です。

3.の領域は、下の図の赤色の直線に対応します。
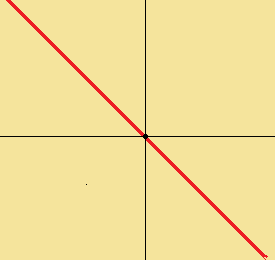
正解は3です。
1と2は$\displaystyle{\mathbb{R}^2}$の線形部分空間ではないので、気をつけてください。
1.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{xy \geqq 0}$を満たすもの全体
2.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{y=0}$でないもの全体
3.ベクトル$\displaystyle{\begin{pmatrix}x\\y\end{pmatrix}}$で、$\displaystyle{x+y=0}$を満たすもの全体
1.の領域は、下の図で青色に塗られた領域を表しています(黒線の領域も含める)。

2.の領域は、下の図で青色に塗られた領域を表しています。つまりx軸だけ取り除いた空間です。

3.の領域は、下の図の赤色の直線に対応します。

正解は3です。
1と2は$\displaystyle{\mathbb{R}^2}$の線形部分空間ではないので、気をつけてください。
自明?な線形部分空間
“線形部分空間”は分かりましたか??
$\displaystyle{W}$が線形空間$\displaystyle{V}$の線形部分空間であるとは↓↓↓
$\displaystyle{W}$が$\displaystyle{V}$の部分集合、つまり$\displaystyle{W \subset V}$であって、
$\displaystyle{W}$自身も、線形空間を成していることです。
“部分集合”というのは、詳しくは集合論でやりますが、
まぁ「$\displaystyle{W}$が$\displaystyle{V}$の部分集合ってのは、$\displaystyle{W}$が$\displaystyle{V}$の一部なんだな〜」
とでも思ってください。
さて、$\displaystyle{V}$を線形空間としたとき、
$\displaystyle{V}$は$\displaystyle{V}$の線形部分空間になります。
つまり、線形部分空間は自身も含めるのです!!
どこかの言葉に部分は全体よりも小さいというのがありますが、
数学の世界では“全体”も“一部分”として考えることがあります。
実際、集合論の考え方的な考え方であっても$\displaystyle{V}$自身も、$\displaystyle{V}$の部分集合と考えます。
つまり$\displaystyle{V \subset V}$なんです。
そう考えると、どんな線形空間$\displaystyle{V}$をとってきても、
その線形部分空間は存在することになります。つまり$\displaystyle{V}$自身です。
このような線形部分空間を“自明な”線形部分空間といいます。
$\displaystyle{W}$が線形空間$\displaystyle{V}$の線形部分空間であるとは↓↓↓
$\displaystyle{W}$が$\displaystyle{V}$の部分集合、つまり$\displaystyle{W \subset V}$であって、
$\displaystyle{W}$自身も、線形空間を成していることです。
“部分集合”というのは、詳しくは集合論でやりますが、
まぁ「$\displaystyle{W}$が$\displaystyle{V}$の部分集合ってのは、$\displaystyle{W}$が$\displaystyle{V}$の一部なんだな〜」
とでも思ってください。
さて、$\displaystyle{V}$を線形空間としたとき、
$\displaystyle{V}$は$\displaystyle{V}$の線形部分空間になります。
つまり、線形部分空間は自身も含めるのです!!
どこかの言葉に部分は全体よりも小さいというのがありますが、
数学の世界では“全体”も“一部分”として考えることがあります。
実際、集合論の考え方的な考え方であっても$\displaystyle{V}$自身も、$\displaystyle{V}$の部分集合と考えます。
つまり$\displaystyle{V \subset V}$なんです。
そう考えると、どんな線形空間$\displaystyle{V}$をとってきても、
その線形部分空間は存在することになります。つまり$\displaystyle{V}$自身です。
このような線形部分空間を“自明な”線形部分空間といいます。
線形部分空間の次元
$\displaystyle{W}$が、線形空間$\displaystyle{V}$の線形部分空間ならば、
$\displaystyle{\mathrm{dim} W \leqq \mathrm{dim}V}$
が必ず成り立ちます。
つまり、線形部分空間の次元は、元の線形空間の次元よりも小さくなる(以下である)、ということですね。
$\displaystyle{\mathrm{dim} W \leqq \mathrm{dim}V}$
が必ず成り立ちます。
つまり、線形部分空間の次元は、元の線形空間の次元よりも小さくなる(以下である)、ということですね。
部分空間
ところで、線形部分空間のことを省略して部分空間ということがあります。
“部分空間”という省略法は、どの教科書でも比較的多く見られます。
しかし、少なくともこのホームページ内では、“線形部分空間”というように、気をつけますm(_ _)m
“部分空間”という省略法は、どの教科書でも比較的多く見られます。
しかし、少なくともこのホームページ内では、“線形部分空間”というように、気をつけますm(_ _)m