記号∀と∃の使い方
Follow @tepika_math∀と∃
ここでは、記号「∀」と「∃」の意味について解説していきたいと思います。
ところで、この記号→「∀」はすっごく見たことがあると思います。ほら、よく顔文字に使われている(笑)
m(≧∀≦)m←こんなカンジ
確かに「∀」は笑った時の口の形に似ているので、笑顔系の顔文字によく使われたりしています。
メールが大好きな方には馴染み深い記号「∀」ですが、この記号の意味を知っている人は案外少ないのでは・・・
数学記号はいろいろな形があるので、本来の目的に反して、顔文字の方により多く使われる・・・悲しい事実です(?)
さてさて、前置きはそのくらいにしておきましょう。
記号「∀」は、アルファベットのAを逆にした記号で、「全ての」という意味になります。ALLの頭文字をとったものです。
記号「∃」は、アルファベットのEを逆にした記号で、「少なくとも一つ存在する」という意味になります。EXISTの頭文字をとったものです。
ところで、この記号→「∀」はすっごく見たことがあると思います。ほら、よく顔文字に使われている(笑)
m(≧∀≦)m←こんなカンジ
確かに「∀」は笑った時の口の形に似ているので、笑顔系の顔文字によく使われたりしています。
メールが大好きな方には馴染み深い記号「∀」ですが、この記号の意味を知っている人は案外少ないのでは・・・
数学記号はいろいろな形があるので、本来の目的に反して、顔文字の方により多く使われる・・・悲しい事実です(?)
さてさて、前置きはそのくらいにしておきましょう。
記号「∀」は、アルファベットのAを逆にした記号で、「全ての」という意味になります。ALLの頭文字をとったものです。
記号「∃」は、アルファベットのEを逆にした記号で、「少なくとも一つ存在する」という意味になります。EXISTの頭文字をとったものです。
使用例
表記の仕方として、
$\displaystyle{\forall x}$や $\displaystyle{\exists x}$と表記し、
それぞれ「全ての$\displaystyle{x}$について〜」や 「〜となる$\displaystyle{x}$が存在する」という意味になります。
また$\displaystyle{x}$を、例えば実数のどれかとしたければ、
$\displaystyle{\forall x \in \mathbb{R}}$
$\displaystyle{\exists x \in \mathbb{R}}$
のようにします。
それでは、使い方を見ていきましょ。
この$\displaystyle{\forall x}$や $\displaystyle{\exists x}$の後に条件文を書いて用います。
例えば、
$\displaystyle{\exists x \in \mathbb{R}, x^2-1=0}$ というように表します。
これはどういう意味かというと
「$\displaystyle{x^2-1}$という条件を満たすような実数$\displaystyle{x}$が存在する」
という意味になります。
この方程式を満たす実数$\displaystyle{x}$は-1と1 になるので、確かにこの命題は正しいことになります。
もちろん、
$\displaystyle{\forall x \in \mathbb{R}, x^2-1=0}$ これはうそっぱちです。
なぜなら、これの意味は
「全ての実数$\displaystyle{x}$に対して$\displaystyle{x^2-1}$が成り立つ」
となってしまいます。
ところで
$\displaystyle{\forall x \in \mathbb{R}, \sin^2 x + \cos^2 x = 1}$
これは正しいです。
なぜなら、どんな$\displaystyle{x}$に対しても上の式が成り立ちます。
$\displaystyle{\forall x}$や $\displaystyle{\exists x}$と表記し、
それぞれ「全ての$\displaystyle{x}$について〜」や 「〜となる$\displaystyle{x}$が存在する」という意味になります。
また$\displaystyle{x}$を、例えば実数のどれかとしたければ、
$\displaystyle{\forall x \in \mathbb{R}}$
$\displaystyle{\exists x \in \mathbb{R}}$
のようにします。
それでは、使い方を見ていきましょ。
この$\displaystyle{\forall x}$や $\displaystyle{\exists x}$の後に条件文を書いて用います。
例えば、
$\displaystyle{\exists x \in \mathbb{R}, x^2-1=0}$ というように表します。
これはどういう意味かというと
「$\displaystyle{x^2-1}$という条件を満たすような実数$\displaystyle{x}$が存在する」
という意味になります。
この方程式を満たす実数$\displaystyle{x}$は-1と1 になるので、確かにこの命題は正しいことになります。
もちろん、
$\displaystyle{\forall x \in \mathbb{R}, x^2-1=0}$ これはうそっぱちです。
なぜなら、これの意味は
「全ての実数$\displaystyle{x}$に対して$\displaystyle{x^2-1}$が成り立つ」
となってしまいます。
ところで
$\displaystyle{\forall x \in \mathbb{R}, \sin^2 x + \cos^2 x = 1}$
これは正しいです。
なぜなら、どんな$\displaystyle{x}$に対しても上の式が成り立ちます。
いくつかの例
それでは、今まで出てきたもののいくつかを記号∀と∃を使って表してみましょう。
$\displaystyle{\mathbb{A}}$が$\displaystyle{\mathbb{B}}$の部分集合の場合を考えましょう。
部分集合とは、別の書き方をすれば、
$\displaystyle{\mathbb{A}\subset\mathbb{B}}$とは、
$\displaystyle{\forall{x},x\in\mathbb{A}{\Rightarrow}x\in\mathbb{B}}$のことである。
となります。
なぜなら、部分集合なので$\displaystyle{\mathbb{A}}$の元は必ず$\displaystyle{\mathbb{B}}$に含まれるからです。
次は、単射の場合を考えましょう。
単射とは、終域の全ての元の逆像は、絶対に複数持つことはありませんでした。
だから、もし$\displaystyle{f(a)=f(b)}$となったら、必ず$\displaystyle{a=b}$とならなければなりません。
もし$\displaystyle{f(a)=f(b)}$なのに$\displaystyle{a{\neq}b}$だったとしたら、単射として、おかしなことになっています。
・・・ということで、単射を∀の記号を使って表すとしたら、
$\displaystyle{f:\mathbb{A}\rightarrow\mathbb{B}}$が単射とは
$\displaystyle{\forall{a,b\in\mathbb{A}},f(a)=f(b)\Rightarrow{a=b}}$が成り立つことである
となります。
それでは、全射の場合はどうなるでしょう?
全射とは、全ての終域の元は必ず逆像を持つことが必要十分でした。
たから、
$\displaystyle{f:\mathbb{A}\rightarrow\mathbb{B}}$が全射とは
$\displaystyle{\forall{b\in\mathbb{B}},\exists{a\in\mathbb{A}}s.t.,f(a)=b}$がなりたつことである
となります。
(時々$\displaystyle{\exists}$の後に$\displaystyle{s.t.}$という記号が来ることがあります。これは"such that"の略です。)
全射の場合は記号∀と∃を同時に使うため、一見分かりにくいかもしれませんが、この記法にも「慣れ」ることが大切です。
$\displaystyle{\mathbb{A}}$が$\displaystyle{\mathbb{B}}$の部分集合の場合を考えましょう。
部分集合とは、別の書き方をすれば、
$\displaystyle{\mathbb{A}\subset\mathbb{B}}$とは、
$\displaystyle{\forall{x},x\in\mathbb{A}{\Rightarrow}x\in\mathbb{B}}$のことである。
となります。
なぜなら、部分集合なので$\displaystyle{\mathbb{A}}$の元は必ず$\displaystyle{\mathbb{B}}$に含まれるからです。
次は、単射の場合を考えましょう。
単射とは、終域の全ての元の逆像は、絶対に複数持つことはありませんでした。
だから、もし$\displaystyle{f(a)=f(b)}$となったら、必ず$\displaystyle{a=b}$とならなければなりません。
もし$\displaystyle{f(a)=f(b)}$なのに$\displaystyle{a{\neq}b}$だったとしたら、単射として、おかしなことになっています。
・・・ということで、単射を∀の記号を使って表すとしたら、
$\displaystyle{f:\mathbb{A}\rightarrow\mathbb{B}}$が単射とは
$\displaystyle{\forall{a,b\in\mathbb{A}},f(a)=f(b)\Rightarrow{a=b}}$が成り立つことである
となります。
それでは、全射の場合はどうなるでしょう?
全射とは、全ての終域の元は必ず逆像を持つことが必要十分でした。
たから、
$\displaystyle{f:\mathbb{A}\rightarrow\mathbb{B}}$が全射とは
$\displaystyle{\forall{b\in\mathbb{B}},\exists{a\in\mathbb{A}}s.t.,f(a)=b}$がなりたつことである
となります。
(時々$\displaystyle{\exists}$の後に$\displaystyle{s.t.}$という記号が来ることがあります。これは"such that"の略です。)
全射の場合は記号∀と∃を同時に使うため、一見分かりにくいかもしれませんが、この記法にも「慣れ」ることが大切です。
二重の∀と∃
例えば、
$\displaystyle{\forall{x},xは\mathrm{YUKI}が好き}$
は、「全ての人はYUKIが好き」という意味になり、
$\displaystyle{\exists{x},xは\mathrm{YUKI}が好き}$
は、「ある人がいて、その人はYUKIが好き」
つまり「YUKIのことが好きな人がいる」という意味になります。
また、
$\displaystyle{\forall{x},\mathrm{YUKI}はxが好き}$
は、「YUKIが全ての人が好き」という意味になり、
$\displaystyle{\exists{x},xは\mathrm{YUKI}が好き}$
は、「YUKIには好きな人がいる」という意味になります。
しかし、以下の場合はどうでしょうか?
$\displaystyle{\forall{x}\exists{y},xはyが好き}$ $\displaystyle{\cdots\cdots(1)}$
$\displaystyle{\exists{y}\forall{x},xはyが好き}$ $\displaystyle{\cdots\cdots(2)}$
このとき、(1)の意味は、「全ての人に好きな人がいる」という意味になり、
(2)の意味は、「全ての人から好かれている人がいる」という意味になります。
図に示すと、以下のようになりますかね?
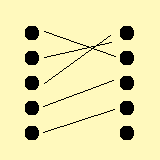
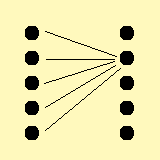
左側が(1)の場合、右側が(2)の場合になると思います。
ただ∀と∃を入れ替えただけで意味が違ってくるということは、とても不思議に感じるかもしれないです。
なぜか∀の後にくる∃は、前の∀に依存してしまいます。
たとえば、∀x∃yとした場合は、xの値によってyが決まる、つまり「全てのxに対してあるyが存在する」という意味に暗黙的になってしまいます。
また∃y∀xとした場合は、xの値に関係なしにyが独立的に決められます。この場合、「全てのxに対して〜というようなyが少なくとも1つ存在する」という意味なります。
混乱しないでください。私も最初は混乱しましたが、そのうちだんだんと分かっていただければいいと思います(-o-;)
ちなみに、
$\displaystyle{\forall{y}\exists{x},xはyが好き}$ $\displaystyle{\cdots\cdots(3)}$
$\displaystyle{\exists{x}\forall{y},xはyが好き}$ $\displaystyle{\cdots\cdots(4)}$
の場合、(3)は「全ての人は誰かから好かれている」になり
(4)は「全ての人が好きな人がいる」となると思います。
さて、以上のことを踏まえて、以下の2つの命題・・・どちらか片方が正解です。
あなたには正解が分かりますか???
$\displaystyle{\forall{x}\in\mathbb{R}, \exists{y}\in\mathbb{R},x{\lt}y}$
$\displaystyle{\exists{y}\in\mathbb{R}, \forall{x}\in\mathbb{R},x{\lt}y}$
上が正解になります。 それぞれ
$\displaystyle{\forall{x},xは\mathrm{YUKI}が好き}$
は、「全ての人はYUKIが好き」という意味になり、
$\displaystyle{\exists{x},xは\mathrm{YUKI}が好き}$
は、「ある人がいて、その人はYUKIが好き」
つまり「YUKIのことが好きな人がいる」という意味になります。
また、
$\displaystyle{\forall{x},\mathrm{YUKI}はxが好き}$
は、「YUKIが全ての人が好き」という意味になり、
$\displaystyle{\exists{x},xは\mathrm{YUKI}が好き}$
は、「YUKIには好きな人がいる」という意味になります。
しかし、以下の場合はどうでしょうか?
$\displaystyle{\forall{x}\exists{y},xはyが好き}$ $\displaystyle{\cdots\cdots(1)}$
$\displaystyle{\exists{y}\forall{x},xはyが好き}$ $\displaystyle{\cdots\cdots(2)}$
このとき、(1)の意味は、「全ての人に好きな人がいる」という意味になり、
(2)の意味は、「全ての人から好かれている人がいる」という意味になります。
図に示すと、以下のようになりますかね?


左側が(1)の場合、右側が(2)の場合になると思います。
ただ∀と∃を入れ替えただけで意味が違ってくるということは、とても不思議に感じるかもしれないです。
なぜか∀の後にくる∃は、前の∀に依存してしまいます。
たとえば、∀x∃yとした場合は、xの値によってyが決まる、つまり「全てのxに対してあるyが存在する」という意味に暗黙的になってしまいます。
また∃y∀xとした場合は、xの値に関係なしにyが独立的に決められます。この場合、「全てのxに対して〜というようなyが少なくとも1つ存在する」という意味なります。
混乱しないでください。私も最初は混乱しましたが、そのうちだんだんと分かっていただければいいと思います(-o-;)
ちなみに、
$\displaystyle{\forall{y}\exists{x},xはyが好き}$ $\displaystyle{\cdots\cdots(3)}$
$\displaystyle{\exists{x}\forall{y},xはyが好き}$ $\displaystyle{\cdots\cdots(4)}$
の場合、(3)は「全ての人は誰かから好かれている」になり
(4)は「全ての人が好きな人がいる」となると思います。
さて、以上のことを踏まえて、以下の2つの命題・・・どちらか片方が正解です。
あなたには正解が分かりますか???
$\displaystyle{\forall{x}\in\mathbb{R}, \exists{y}\in\mathbb{R},x{\lt}y}$
$\displaystyle{\exists{y}\in\mathbb{R}, \forall{x}\in\mathbb{R},x{\lt}y}$
上が正解になります。 それぞれ
- どんな実数xに対しても、それよりも大きい実数yが存在する
- いかなる数よりも大きな実数yが存在する