対応先の元のことを像といいます。

今度は、以下の例を見ていきましょう。

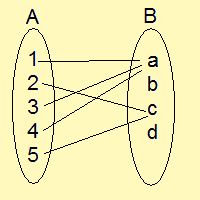
この例では、1はaに、2はcに・・・というように対応されています。
よって1の像はaに、2の像はcとなります。


また、
$\displaystyle{\{f(a)|a\in\mathbb{A}\}}$
のことを、集合$\displaystyle{\mathbb{A}}$の像ともいい、
$\displaystyle{f(\mathbb{A})}$
と表したりもします。
この図でいうと、集合$\displaystyle{\mathbb{A}}$の像は、全ての元がaとcに対応されているので、
$\displaystyle{\{a,c\}}$

となります。

始域（この例では集合$\displaystyle{\mathbb{A}}$）の像は、終域（この例では集合$\displaystyle{\mathbb{B}}$）の部分集合になることが分かります。
気をつけるのは、「像」という用語は、「対応先の元」のことと、「その写像が描く終域の部分集合」 の二つの意味合いがあることです。
後者は、値域と呼ぶことがあります。

像は分かりましたか？

像とは、対応先のことです。
そこで、今度は逆像のことを考えましょう。
像が「対応先」だとすれば、逆像は「対応元」のことです。

もう一回この図を用意します。

この図では、aの逆像は｛1,3,4｝です。なぜなら、aは1と3と4から対応されているからです。
このように、逆像とは像の逆関係にあります。
また、cの逆像は｛2,5｝であることは分かりますよね？

$\displaystyle{f}$が$\displaystyle{\mathbb{A}}$から$\displaystyle{\mathbb{B}}$への写像のとき、
その逆像（$\displaystyle{\mathbb{A}}$の部分集合に移す）は、
$\displaystyle{f^{-1}(x)}$
のように、-1をつけると、その写像の逆像を表すことになります。
例えば、aの逆像は、
$\displaystyle{f^{-1}(a)=\{1,3,4\}}$
となります。

また$\displaystyle{\mathbb{B}'\subset\mathbb{B}}$として、

$\displaystyle{f^{-1}(\mathbb{B}')=\{a\in\mathbb{A}|f(a)\in\mathbb{B}'\}}$

というように記述することもできます。

もし、
$\displaystyle{\mathbb{B}'=\{a,c\}}$
としたら、
$\displaystyle{f^{-1}(\mathbb{B}')=\{1,2,3,4,5\}=\mathbb{A}}$

となることが分かると思います。