全射と単射
Follow @tepika_math全射とは?
像と逆像でやったように、始域の像は終域の部分集合となります。
しかし、始域の像と終域が一致するとき、この写像のことを全射といいます。
・・・なぁんて言われても分かりにくいと思うので、実際に例を出していきます。
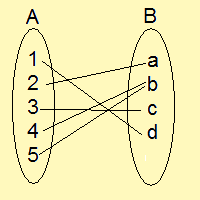
まずは左側の写像の例から見ていきましょうか?
左側の写像では、
$\displaystyle{f(\mathbb{A})=\{a,b,c,d\}=\mathbb{B}}$
となり、見事に$\displaystyle{\mathbb{A}}$の像が$\displaystyle{\mathbb{B}}$に一致しています。
これが全射です!!!
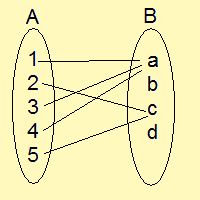
しかし、右側の写像では、
$\displaystyle{f(\mathbb{A})=\{a,c\}\neq\mathbb{B}}$
のように、bとdには対応する逆像がありません。よってこれは全射ではありません。
つまり全射とは「終域の元全てに逆像が存在する」ような写像のことをいうのです。
また、全射は始域の像が見事に終域の元に一致するので、上への写像と呼ばれることがあります。
ところで、
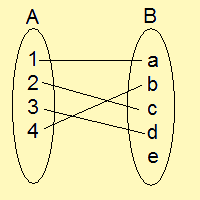
のような写像があるとしましょう。
この$\displaystyle{\mathbb{A}}$と$\displaystyle{\mathbb{B}}$に関しては、 どのように写像を選び直しても全射になることができません。
それもそのはず、始域の元の数よりも終域の元の数の方が多いため、写像をどのようにとっても終域の元が余ってしまうからです。
つまり、始域の元の数よりも終域の元の数の方が多い場合、全射をとることはできません。
しかし、始域の像と終域が一致するとき、この写像のことを全射といいます。
・・・なぁんて言われても分かりにくいと思うので、実際に例を出していきます。


まずは左側の写像の例から見ていきましょうか?
左側の写像では、
$\displaystyle{f(\mathbb{A})=\{a,b,c,d\}=\mathbb{B}}$
となり、見事に$\displaystyle{\mathbb{A}}$の像が$\displaystyle{\mathbb{B}}$に一致しています。
これが全射です!!!
しかし、右側の写像では、
$\displaystyle{f(\mathbb{A})=\{a,c\}\neq\mathbb{B}}$
のように、bとdには対応する逆像がありません。よってこれは全射ではありません。
つまり全射とは「終域の元全てに逆像が存在する」ような写像のことをいうのです。
また、全射は始域の像が見事に終域の元に一致するので、上への写像と呼ばれることがあります。
ところで、

のような写像があるとしましょう。
この$\displaystyle{\mathbb{A}}$と$\displaystyle{\mathbb{B}}$に関しては、 どのように写像を選び直しても全射になることができません。
それもそのはず、始域の元の数よりも終域の元の数の方が多いため、写像をどのようにとっても終域の元が余ってしまうからです。
つまり、始域の元の数よりも終域の元の数の方が多い場合、全射をとることはできません。
単射とは?
全ての終域の元の逆像が高々1個(多くても1個という意味。つまり0個の場合でもよい)しか存在しないとき、この写像のことを単射といいます。
また図に示してみましょう。

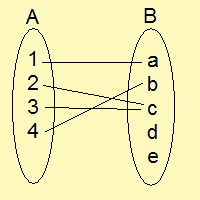
左側の写像は単射になりますが、右側は単射ではありません。
右側の写像の例で、終域の元cを見てみますと、cの逆像は2と3と、2つ存在します。
このように、終域の元の中に一つでも、逆像が複数あるものが存在すれば単射とはいえません。
そのかわり、左側の写像の例を見ますと、終域の元のうち逆像が複数あるものは1つもありません。
ところで、左側の終域のeという元は逆像がありませんが、高々1つの逆像を持てばいいので、逆像を持ってない場合でもOKです!!
また、単射は1対1の写像と呼ばれることがあります。
ところで、
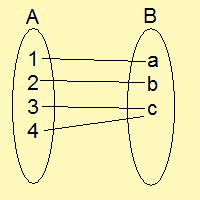
のような写像があるとしましょう。
なんとなく分かると思いますが、この$\displaystyle{\mathbb{A}}$と$\displaystyle{\mathbb{B}}$では、 どのように写像をとっても単射を作ることができません。
なぜなら、始域よりも終域が少ないため、始域の元を全て終域に対応させようとすると、どうしても対応が重なってしまうからです。
だから、始域の元の数よりも終域の元の数の方が少ない場合、単射をとることはできません
また図に示してみましょう。


左側の写像は単射になりますが、右側は単射ではありません。
右側の写像の例で、終域の元cを見てみますと、cの逆像は2と3と、2つ存在します。
このように、終域の元の中に一つでも、逆像が複数あるものが存在すれば単射とはいえません。
そのかわり、左側の写像の例を見ますと、終域の元のうち逆像が複数あるものは1つもありません。
ところで、左側の終域のeという元は逆像がありませんが、高々1つの逆像を持てばいいので、逆像を持ってない場合でもOKです!!
また、単射は1対1の写像と呼ばれることがあります。
ところで、

のような写像があるとしましょう。
なんとなく分かると思いますが、この$\displaystyle{\mathbb{A}}$と$\displaystyle{\mathbb{B}}$では、 どのように写像をとっても単射を作ることができません。
なぜなら、始域よりも終域が少ないため、始域の元を全て終域に対応させようとすると、どうしても対応が重なってしまうからです。
だから、始域の元の数よりも終域の元の数の方が少ない場合、単射をとることはできません