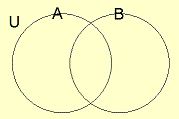
ベン図とは、以下のように、集合を図を用いて少し分かりやすくしたものです。

この図では、左側の円は、集合$\displaystyle{\mathbb{A}}$を、 右側の円は、集合$\displaystyle{\mathbb{B}}$を表しています。
その円の中に$\displaystyle{\mathbb{A}}$元や$\displaystyle{\mathbb{B}}$の元が含まれているのだと思ってください。
また、普遍集合を集合$\displaystyle{\mathbb{U}}$としてることが分かると思います。



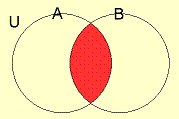
さて、集合$\displaystyle{\mathbb{A}}$と集合$\displaystyle{\mathbb{B}}$の共通部分、つまり $\displaystyle{\mathbb{A}\cap\mathbb{B}}$は、この図でいうと、どこになるのでしょうか？
共通部分は以下の図のように二つの円で重なった、赤色の部分だということが分かります。




それでは、集合$\displaystyle{\mathbb{A}}$と集合$\displaystyle{\mathbb{B}}$の和集合 $\displaystyle{\mathbb{A}\cup\mathbb{B}}$は、この図でいうと、どこの部分を指すのでしょうか？
和集合は、以下のような領域であることが分かると思います。

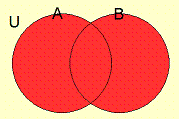
このように、 ベン図を使えば二つの集合を視覚的に表現することができます。

さて、ここで集合論においてとても有名なド・モルガンの法則というものを紹介しましょう。
集合論において、以下の法則が成り立ちます。
$\displaystyle{\overline{(\mathbb{A}\cap\mathbb{B})}=\overline{\mathbb{A}}\cup\overline{\mathbb{B}}}$$\displaystyle{\cdots\cdots(1)}$
$\displaystyle{\overline{(\mathbb{A}\cup\mathbb{B})}=\overline{\mathbb{A}}\cap\overline{\mathbb{B}}}$$\displaystyle{\cdots\cdots(2)}$
この法則は、是非覚えておきましょう。

さて、この法則の証明ですが、ベン図を使えばとても簡単に証明できます。
まずは、(1)から証明していきましょう。

(1)の左辺、つまり$\displaystyle{\overline{(\mathbb{A}\cap\mathbb{B})}}$は、 集合$\displaystyle{\mathbb{A}}$と集合$\displaystyle{\mathbb{B}}$の共通部分の補集合であるので、 ベン図で表すと以下の赤い部分になります。

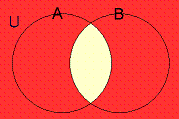
これが$\displaystyle{\overline{\mathbb{A}}}$と$\displaystyle{\overline{\mathbb{B}}}$の和集合になることを示せばよいのですが・・・。
まず$\displaystyle{\overline{\mathbb{A}}}$は

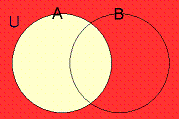
となり、
$\displaystyle{\overline{\mathbb{B}}}$が

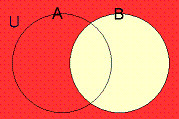
となるため、
これらの和集合は、

$\displaystyle{\cup}$$\displaystyle{=}$

となることが分かると思います。もしよかったら、自分でベン図を作って実際に確かめるのもよいかもしれません。

もし余裕がありましたら、(2)の場合も試してみましょう。。。