直径
Follow @tepika_math直径とは?
$\displaystyle{\mathbb{X}}$
に距離$\displaystyle{d}$が定義されているとします。
今回は$\displaystyle{\mathbb{A}\subset\mathbb{X}}$のように、 $\displaystyle{\mathbb{X}}$の部分集合を考えていきたいと思います。
$\displaystyle{d(\mathbb{A})=\sup\{d(x,y)|x,y\in\mathbb{A}\}}$
なる量$\displaystyle{d(\mathbb{A})}$のことを、 $\displaystyle{\mathbb{A}}$の直径といいます。
直観的に言えば、$\displaystyle{d(\mathbb{A})}$とは 『一番遠く離れた点同士の距離』みたいなものだと考えてください。
今回は$\displaystyle{\mathbb{A}\subset\mathbb{X}}$のように、 $\displaystyle{\mathbb{X}}$の部分集合を考えていきたいと思います。
$\displaystyle{d(\mathbb{A})=\sup\{d(x,y)|x,y\in\mathbb{A}\}}$
なる量$\displaystyle{d(\mathbb{A})}$のことを、 $\displaystyle{\mathbb{A}}$の直径といいます。
直観的に言えば、$\displaystyle{d(\mathbb{A})}$とは 『一番遠く離れた点同士の距離』みたいなものだと考えてください。
例(1次元ユークリッド距離)
例えば、
実数の集合$\displaystyle{\mathbb{R}}$の通常の位相において、
実数の部分集合$\displaystyle{[-1,3]}$の直径は4です。
なぜなら、直径とは、直観的には一番遠く離れた点同士の距離という感じですので、
3と−1が一番遠く離れた点だというのは分かると思います。
だから3と−1の距離は4なので、直径の値が4になります。
次に $\displaystyle{(2,5)}$の直径は3です。
ところで、直径とは何度も言うように『一番遠く離れた点同士の距離』という感じですが、
この例のときは2と5が一番遠く離れていそうです。
でも・・・2と5は$\displaystyle{(2,5)}$の元ではありません。
しかし、直径は「点同士の距離の最大値」ではなく「点同士の距離の上限」なので、直径は3でいいのです。
実数の集合$\displaystyle{\mathbb{R}}$の通常の位相において、
実数の部分集合$\displaystyle{[-1,3]}$の直径は4です。
なぜなら、直径とは、直観的には一番遠く離れた点同士の距離という感じですので、
3と−1が一番遠く離れた点だというのは分かると思います。
だから3と−1の距離は4なので、直径の値が4になります。
次に $\displaystyle{(2,5)}$の直径は3です。
ところで、直径とは何度も言うように『一番遠く離れた点同士の距離』という感じですが、
この例のときは2と5が一番遠く離れていそうです。
でも・・・2と5は$\displaystyle{(2,5)}$の元ではありません。
しかし、直径は「点同士の距離の最大値」ではなく「点同士の距離の上限」なので、直径は3でいいのです。
例(2次元ユークリッド距離)
また二次元平面$\displaystyle{\mathbb{R}^2}$上で定義された
ユークリッド距離を考えるとすると、
下の絵のピンク色で表わされた集合の直径(境界は含まないものとする)は $\displaystyle{2\delta}$となります。
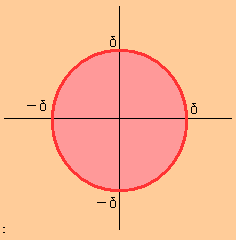
・・・境界を含んでいなかったとしても、
「最大値」ではなくて「上限」なので、大丈夫ですね。
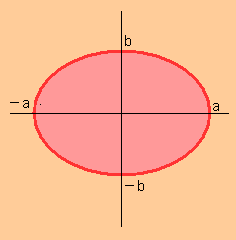
また、下の絵のピンク色で表わされた集合の直径は
(境界は含まないものとする・・・まぁ境界を含んでも前みたいに結果は同じですが)
$\displaystyle{2a}$となります。
次に、下の絵のピンク色で表わされた集合の直径は、青色の線の長さになります。
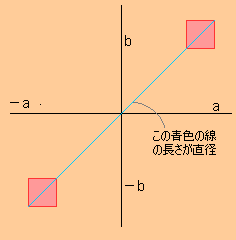
このように、連結でない(いくつかに分離されている)領域でも、直径は定義されています。
下の絵のピンク色で表わされた集合の直径(境界は含まないものとする)は $\displaystyle{2\delta}$となります。

・・・境界を含んでいなかったとしても、
「最大値」ではなくて「上限」なので、大丈夫ですね。
また、下の絵のピンク色で表わされた集合の直径は
(境界は含まないものとする・・・まぁ境界を含んでも前みたいに結果は同じですが)
$\displaystyle{2a}$となります。

次に、下の絵のピンク色で表わされた集合の直径は、青色の線の長さになります。

このように、連結でない(いくつかに分離されている)領域でも、直径は定義されています。
開球の直径
前回は開球というものをやりました。
覚えていますか?
中心$\displaystyle{x}$で 半径$\displaystyle{\delta}$の開球を
$\displaystyle{U_\delta(x)}$
で表わしましたが、
この開球の直径は
$\displaystyle{d(U_\delta(x)) \leqq 2 \delta}$
とはなりますが(証明)
$\displaystyle{d(U_\delta(x))=2\delta}$
になるとは限りません。
つまり、中心$\displaystyle{x}$で 半径$\displaystyle{\delta}$の開球の直径は $\displaystyle{2\delta}$であるとは限らないのです!!!
確かに、ユークリッド距離では、
$\displaystyle{d(U_\delta(x)) = 2 \delta}$
が成り立ちますが・・・そうでない距離では、うまくいかないことがあります。
例えば$\displaystyle{\mathbb{X}}$に 自明な距離(何それって人はココへ)が定義されているとき、
$\displaystyle{d(U_\delta(x))}$
の値は、
$\displaystyle{\delta \lt 1}$のとき$\displaystyle{0}$
$\displaystyle{\delta \geqq 1}$のとき$\displaystyle{1}$
となります。
全然直径の値は$\displaystyle{2\delta}$じゃないですよね?
(注:$\displaystyle{\mathbb{X}}$の元の数が2以上と仮定します。そうじゃないと・・・)
覚えていますか?
中心$\displaystyle{x}$で 半径$\displaystyle{\delta}$の開球を
$\displaystyle{U_\delta(x)}$
で表わしましたが、
この開球の直径は
$\displaystyle{d(U_\delta(x)) \leqq 2 \delta}$
とはなりますが(証明)
$\displaystyle{d(U_\delta(x))=2\delta}$
になるとは限りません。
つまり、中心$\displaystyle{x}$で 半径$\displaystyle{\delta}$の開球の直径は $\displaystyle{2\delta}$であるとは限らないのです!!!
確かに、ユークリッド距離では、
$\displaystyle{d(U_\delta(x)) = 2 \delta}$
が成り立ちますが・・・そうでない距離では、うまくいかないことがあります。
例えば$\displaystyle{\mathbb{X}}$に 自明な距離(何それって人はココへ)が定義されているとき、
$\displaystyle{d(U_\delta(x))}$
の値は、
$\displaystyle{\delta \lt 1}$のとき$\displaystyle{0}$
$\displaystyle{\delta \geqq 1}$のとき$\displaystyle{1}$
となります。
全然直径の値は$\displaystyle{2\delta}$じゃないですよね?
(注:$\displaystyle{\mathbb{X}}$の元の数が2以上と仮定します。そうじゃないと・・・)
有界
もし
$\displaystyle{\{d(x,y) | x,y\in\mathbb{A}\}}$
が上に有界でないとき、
$\displaystyle{d(\mathbb{A})=\sup\{d(x,y)|x,y\in\mathbb{A}\}}$
の$\displaystyle{d(\mathbb{A})}$は値を持ちません。
(↑あるいは$\displaystyle{d(\mathbb{A})=\infty}$となり、無限大に発散してしまいます。)
このとき、$\displaystyle{\mathbb{A}}$は有界でないといいます。
$\displaystyle{d(\mathbb{A})=\infty}$ではないとき、
$\displaystyle{\mathbb{A}}$は有界であるといいます。
例えば、ユークリッド距離で二次元平面全体の集合$\displaystyle{\mathbb{R}^2}$ は、有界ではないですね?
$\displaystyle{\{d(x,y) | x,y\in\mathbb{A}\}}$
が上に有界でないとき、
$\displaystyle{d(\mathbb{A})=\sup\{d(x,y)|x,y\in\mathbb{A}\}}$
の$\displaystyle{d(\mathbb{A})}$は値を持ちません。
(↑あるいは$\displaystyle{d(\mathbb{A})=\infty}$となり、無限大に発散してしまいます。)
このとき、$\displaystyle{\mathbb{A}}$は有界でないといいます。
$\displaystyle{d(\mathbb{A})=\infty}$ではないとき、
$\displaystyle{\mathbb{A}}$は有界であるといいます。
例えば、ユークリッド距離で二次元平面全体の集合$\displaystyle{\mathbb{R}^2}$ は、有界ではないですね?