集合間の距離
Follow @tepika_math集合と集合の距離
前回は、距離空間の部分集合において「直径」というものを定義しました。
直径とは、一番距離が離れている点との距離だと思ってください。
今回は、二つの距離空間における距離というものを考えていきます。
さて$\displaystyle{A}$を距離空間とし、その距離を$\displaystyle{d}$とします。
そして$\displaystyle{X,Y}$を距離空間$\displaystyle{A}$の部分集合とします。
このとき
$\displaystyle{d(X,Y)=\inf\{d(x,y) | x \in X , y \in Y \}}$
を$\displaystyle{X}$と$\displaystyle{Y}$の距離と定義します。
つまりこーゆーこと(..)φ
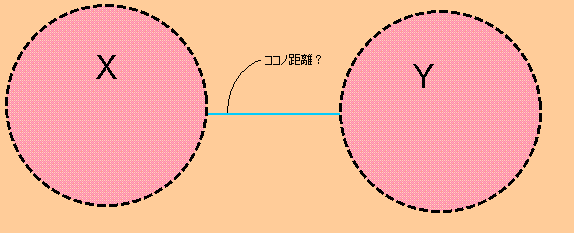
上の図のように、$\displaystyle{X}$を左のピンク色の円、 $\displaystyle{Y}$を右のピンクの円としましょう、
この図が表しているように、
$\displaystyle{X}$と$\displaystyle{Y}$の距離というものは、 一番近い(一番小さな値をとる)距離のことだと思ってください。
確かに$\displaystyle{\inf}$というのは、最小値みたいなものです。
(infは本当は最小値ではなく、下限というものです。詳しくは上限と下限を見て下さい)。
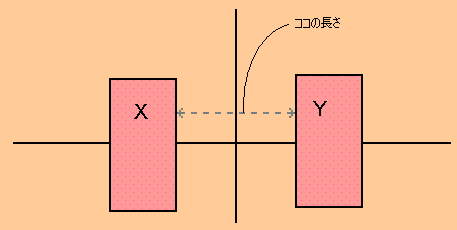
もし$\displaystyle{X,Y}$が以上のような長方形の形の時、
上に図で示された矢印の長さが$\displaystyle{X,Y}$の距離となります。
直径とは、一番距離が離れている点との距離だと思ってください。
今回は、二つの距離空間における距離というものを考えていきます。
さて$\displaystyle{A}$を距離空間とし、その距離を$\displaystyle{d}$とします。
そして$\displaystyle{X,Y}$を距離空間$\displaystyle{A}$の部分集合とします。
このとき
$\displaystyle{d(X,Y)=\inf\{d(x,y) | x \in X , y \in Y \}}$
を$\displaystyle{X}$と$\displaystyle{Y}$の距離と定義します。
つまりこーゆーこと(..)φ

上の図のように、$\displaystyle{X}$を左のピンク色の円、 $\displaystyle{Y}$を右のピンクの円としましょう、
この図が表しているように、
$\displaystyle{X}$と$\displaystyle{Y}$の距離というものは、 一番近い(一番小さな値をとる)距離のことだと思ってください。
確かに$\displaystyle{\inf}$というのは、最小値みたいなものです。
(infは本当は最小値ではなく、下限というものです。詳しくは上限と下限を見て下さい)。

もし$\displaystyle{X,Y}$が以上のような長方形の形の時、
上に図で示された矢印の長さが$\displaystyle{X,Y}$の距離となります。
二つの図形が重なっている時
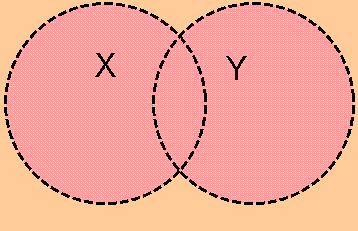
例えば、以上のように二つの図形が重なっているときは、
$\displaystyle{d(X,Y)=0}$
となることが(直観的に)分かると思います。
「重なっているわけだから、お互いの距離は0になるのは当たり前じゃん!!!」
と思うかもしれませんが、数学では直感は禁物です。
少し詳しく見ていきましょう。
$\displaystyle{X,Y}$は重なっているので、
$\displaystyle{a\in{X \cap Y}}$つまり $\displaystyle{a \in X}$かつ$\displaystyle{a \in Y}$と なる元$\displaystyle{a}$の存在が保障されます。
$\displaystyle{d(a,a)=0}$が成り立ちます(距離の公理より)。
$\displaystyle{d(a,a) \in \{d(x,y) | x{\in}X , y{\in}Y \}}$なので、
よって$\displaystyle{\{d(x,y) | x{\in}X , y{\in}Y \}}$は0を含むことになります。
また、距離の公理を参照すれば分かることですが、
$\displaystyle{d(a,b)}$は必ず0より大きな値で、マイナスの値は絶対にとりません。
つまり$\displaystyle{\{d(x,y) | x{\in}X , y{\in}Y \}}$の最小元は0そのものになり、
$\displaystyle{\min\{d(x,y) | x{\in}X , y{\in}Y \} = 0}$
となります。よって
$\displaystyle{\inf\{d(x,y) | x{\in}X , y{\in}Y \} = 0}$
となることがわかりました。
ここで、
$\displaystyle{A}$に最小値が存在するならば
$\displaystyle{\inf{A} = \min{A}}$
となるという性質を使いました。
・・・直感的に分かることでも、こうして数学的に示すことは、少々面倒くさいものですね・・・?
逆の場合
以上、$\displaystyle{X{\cap}Y \neq\phi}$ならば$\displaystyle{d(X,Y)=0}$でした。
ならば逆は言えるのか・・・?
つまり$\displaystyle{d(X,Y)=0}$ならば $\displaystyle{X}$と$\displaystyle{Y}$ は重なっているよ!!!!!
ということが言えるのでしょうか?
実はこれには反例があります。
例えば$\displaystyle{X}$を$\displaystyle{(0,-1)}$ を中心とした境界を含まない半径1の円とし、
同様に$\displaystyle{Y}$を$\displaystyle{(0,1)}$ を中心とした境界を含まない半径1の円とします。
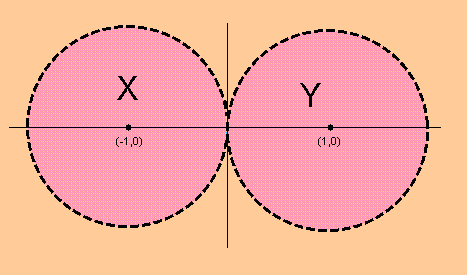
このグラフ、見て分かると思うのですが・・・
原点の部分でくっついている・・・でも二つの円は境界を含まないため、
原点は二つの円にふくまれません。
確かに2つの円の距離は0なのですが、ビミョーな所で重なっていないのです。。。
上手く考えましたね・・・
ならば逆は言えるのか・・・?
つまり$\displaystyle{d(X,Y)=0}$ならば $\displaystyle{X}$と$\displaystyle{Y}$ は重なっているよ!!!!!
ということが言えるのでしょうか?
実はこれには反例があります。
例えば$\displaystyle{X}$を$\displaystyle{(0,-1)}$ を中心とした境界を含まない半径1の円とし、
同様に$\displaystyle{Y}$を$\displaystyle{(0,1)}$ を中心とした境界を含まない半径1の円とします。
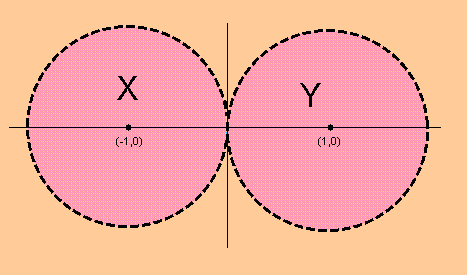
このグラフ、見て分かると思うのですが・・・
原点の部分でくっついている・・・でも二つの円は境界を含まないため、
原点は二つの円にふくまれません。
確かに2つの円の距離は0なのですが、ビミョーな所で重なっていないのです。。。
上手く考えましたね・・・
逆の場合2
ならば境界をもたないからいけないんだ!!!
$\displaystyle{X,Y}$が閉集合、つまり境界を含む集合ならば・・・?
と思うかもしれませんが・・・
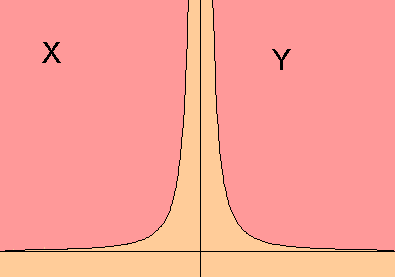
を見て下さい。
これは$\displaystyle{y=\frac{1}{x^2}}$のグラフです。
上に行けば行くほど、お互いの領域が限りなく近づく様子を表現したつもりですが・・・
この場合も、当然お互い交り合う部分はないのですが、距離はゼロになりますね?
$\displaystyle{X,Y}$が閉集合、つまり境界を含む集合ならば・・・?
と思うかもしれませんが・・・

を見て下さい。
これは$\displaystyle{y=\frac{1}{x^2}}$のグラフです。
上に行けば行くほど、お互いの領域が限りなく近づく様子を表現したつもりですが・・・
この場合も、当然お互い交り合う部分はないのですが、距離はゼロになりますね?