近傍
Follow @tepika_math近傍とは
$\displaystyle{X}$を位相空間とします。
そして$\displaystyle{a{\in}X}$とします。
さて、これからは「$\displaystyle{a}$の近傍」など、 「○○の近傍」という、近傍という言葉が出てきます。
さて、その近傍の定義を下に書きます。
そして$\displaystyle{a{\in}X}$とします。
さて、これからは「$\displaystyle{a}$の近傍」など、 「○○の近傍」という、近傍という言葉が出てきます。
さて、その近傍の定義を下に書きます。
近傍の定義
$\displaystyle{A{\subset}X}$として、
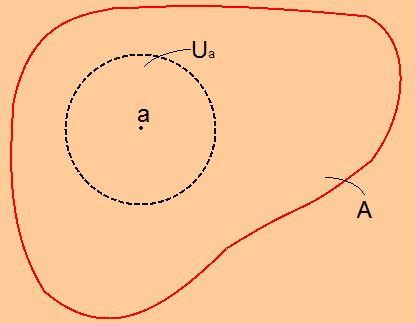
$\displaystyle{A}$が$\displaystyle{a}$の近傍 とは、 ある開集合$\displaystyle{U_a}$が存在して、
$\displaystyle{a{\in}U_a{\subset}A}$
となることである
↑これが近傍の定義です。
・・・よく分からなかった人はいますか???
$\displaystyle{a}$を元ととしてもつ 開集合$\displaystyle{U_a}$があるとしたとき、
$\displaystyle{U_a}$を部分集合としてもつもの なんでも$\displaystyle{a}$の近傍だということです。
$\displaystyle{A}$が$\displaystyle{a}$の近傍 とは、 ある開集合$\displaystyle{U_a}$が存在して、
$\displaystyle{a{\in}U_a{\subset}A}$
となることである
↑これが近傍の定義です。
・・・よく分からなかった人はいますか???
$\displaystyle{a}$を元ととしてもつ 開集合$\displaystyle{U_a}$があるとしたとき、
$\displaystyle{U_a}$を部分集合としてもつもの なんでも$\displaystyle{a}$の近傍だということです。

1次元の位相空間で例を
実数$\displaystyle{\mathbb{R}}$に通常の位相が入っているとします。
さて、0は実数$\displaystyle{\mathbb{R}}$の元ですが、
0の近傍はどんなものになるでしょうか?
0を含む開集合といえば
$\displaystyle{(-1,1)}$
$\displaystyle{(-100,100)}$
$\displaystyle{(-1,1)\cup(2,4)}$
$\displaystyle{(-\infty,\infty)=\mathbb{R}}$
など、いろいろなものが考えられます。
これらを部分集合として含むものは、どんなものでも近傍です。
たとえば閉区間$\displaystyle{[-1,1]}$は
$\displaystyle{(-1,1)\subset[-1,1]}$なので、
$\displaystyle{[-1,1]}$は0の近傍です。
それに$\displaystyle{(-1,1)\cup\{10000000\}}$も0の近傍だし、
$\displaystyle{\mathbb{R}}$自身も0の近傍になります。
当然$\displaystyle{(-1,1)}$自身も0の近傍ですよね?
・・・と考えると、“近傍”っていかにも「近そう」なニュアンスを含めた言葉ですけど、
全然近くありませんね。
一体何なんだ・・・この用語は(・。・)
さて、0は実数$\displaystyle{\mathbb{R}}$の元ですが、
0の近傍はどんなものになるでしょうか?
0を含む開集合といえば
$\displaystyle{(-1,1)}$
$\displaystyle{(-100,100)}$
$\displaystyle{(-1,1)\cup(2,4)}$
$\displaystyle{(-\infty,\infty)=\mathbb{R}}$
など、いろいろなものが考えられます。
これらを部分集合として含むものは、どんなものでも近傍です。
たとえば閉区間$\displaystyle{[-1,1]}$は
$\displaystyle{(-1,1)\subset[-1,1]}$なので、
$\displaystyle{[-1,1]}$は0の近傍です。
それに$\displaystyle{(-1,1)\cup\{10000000\}}$も0の近傍だし、
$\displaystyle{\mathbb{R}}$自身も0の近傍になります。
当然$\displaystyle{(-1,1)}$自身も0の近傍ですよね?
・・・と考えると、“近傍”っていかにも「近そう」なニュアンスを含めた言葉ですけど、
全然近くありませんね。
一体何なんだ・・・この用語は(・。・)
1次元の位相空間で近傍じゃないものの例
逆に以下に挙げるものは0の近傍ではありません。
$\displaystyle{A=\{0\}}$
$\displaystyle{B=\{-1,0,1\}}$
$\displaystyle{C=(-\infty,-1) \cup \{0\} \cup (1,\infty)}$
$\displaystyle{D=[0,3]}$
0の近傍というのは、0を含む開集合を入れることができるか、ということです。
明らかに「この中に、どうやって開集合をいれるんだよ(-o-#) 」っていうものばかりなので、
これらは0の近傍ではありませんよね?
例えば$\displaystyle{A=\{0\}}$の中には、 どうやっても開集合は絶対に入りませんよね。
また、閉区間 $\displaystyle{D=[0,3]}$は0の近傍ではありません。
0を含む開集合をDの中に入れようとしたら、どうしても左側がはみ出してしまいますよね・・・?

$\displaystyle{A=\{0\}}$
$\displaystyle{B=\{-1,0,1\}}$
$\displaystyle{C=(-\infty,-1) \cup \{0\} \cup (1,\infty)}$
$\displaystyle{D=[0,3]}$
0の近傍というのは、0を含む開集合を入れることができるか、ということです。
明らかに「この中に、どうやって開集合をいれるんだよ(-o-#) 」っていうものばかりなので、
これらは0の近傍ではありませんよね?
例えば$\displaystyle{A=\{0\}}$の中には、 どうやっても開集合は絶対に入りませんよね。
また、閉区間 $\displaystyle{D=[0,3]}$は0の近傍ではありません。
0を含む開集合をDの中に入れようとしたら、どうしても左側がはみ出してしまいますよね・・・?

開近傍
さてと・・・。
$\displaystyle{X}$を位相空間とします。
ここで、$\displaystyle{U_a}$を開集合としましょう。
このとき、もし$\displaystyle{a{\in}U_a}$ならば、
$\displaystyle{U_a}$は$\displaystyle{a}$の近傍ですよね?
つまり、
開集合自身も、近傍となるのです。
このことは、近傍の定義をもう一度確認してみれば、分かることですね↓↓↓
(↑数学は、定義に振り返ってみることが大切です!!)
$\displaystyle{U_a}$が$\displaystyle{a}$の近傍 とは、 ある開集合$\displaystyle{O}$が存在して、
$\displaystyle{a{\in}O{\subset}U_a}$
となることである・・・
このときの$\displaystyle{O}$を$\displaystyle{U_a}$とおけばよいのです。
開集合である近傍のことを開近傍といいます。
$\displaystyle{X}$を位相空間とします。
ここで、$\displaystyle{U_a}$を開集合としましょう。
このとき、もし$\displaystyle{a{\in}U_a}$ならば、
$\displaystyle{U_a}$は$\displaystyle{a}$の近傍ですよね?
つまり、
開集合自身も、近傍となるのです。
このことは、近傍の定義をもう一度確認してみれば、分かることですね↓↓↓
(↑数学は、定義に振り返ってみることが大切です!!)
$\displaystyle{U_a}$が$\displaystyle{a}$の近傍 とは、 ある開集合$\displaystyle{O}$が存在して、
$\displaystyle{a{\in}O{\subset}U_a}$
となることである・・・
このときの$\displaystyle{O}$を$\displaystyle{U_a}$とおけばよいのです。
開集合である近傍のことを開近傍といいます。