開球
Follow @tepika_math開球
集合$\displaystyle{\mathbb{X}}$
に距離$\displaystyle{d}$が定義されているとします。
このとき、$\displaystyle{\mathbb{X}}$ の元$\displaystyle{p}$、 正の実数$\displaystyle{\delta}$として、
$\displaystyle{p}$からの距離が $\displaystyle{\delta}$より小さい元を全て集めたものを、
中心$\displaystyle{p}$半径$\displaystyle{\delta}$の 開球いい、
$\displaystyle{U_\delta(p)}$
と表します。
つまり、
$\displaystyle{U_\delta(p)=\{x\in\mathbb{X} | d(x,p) \le \delta\}}$
です。
このとき、$\displaystyle{\mathbb{X}}$ の元$\displaystyle{p}$、 正の実数$\displaystyle{\delta}$として、
$\displaystyle{p}$からの距離が $\displaystyle{\delta}$より小さい元を全て集めたものを、
中心$\displaystyle{p}$半径$\displaystyle{\delta}$の 開球いい、
$\displaystyle{U_\delta(p)}$
と表します。
つまり、
$\displaystyle{U_\delta(p)=\{x\in\mathbb{X} | d(x,p) \le \delta\}}$
です。
開球の例
$\displaystyle{\mathbb{R}^2}$
つまり平面の場合を考えてみましょう。
例えば$\displaystyle{d}$をユークリッド距離
$\displaystyle{d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}}$
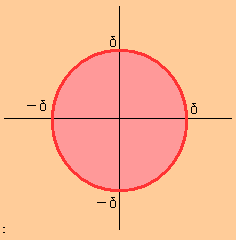
とすれば、$\displaystyle{U_\delta(0)}$は原点中心の半径$\displaystyle{\delta}$の円になります。
もちろん「開球」の定義を見れば分かる通り、円周は含みませんが・・・
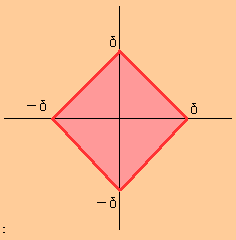
また$\displaystyle{d(x,y)=|x_1-y_1|+|x_2-y_2|}$ とすれば、$\displaystyle{U_\delta(0)}$はダイヤの形になります。
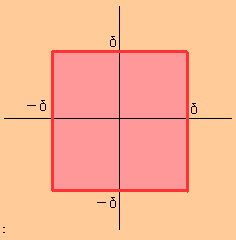
また$\displaystyle{d(x,y)=\max\{|x_1-y_1|,|x_2-y_2|\}}$ とすれば、$\displaystyle{U_\delta(0)}$は正方形になります。
次に$\displaystyle{d}$を自明な距離とすると(←自明な距離の説明はココ!)
$\displaystyle{\delta \lt 1}$のとき、 $\displaystyle{U_\delta(0)}$ は集合$\displaystyle{\{0\}}$つまり一つの元だけからなる集合になります。
$\displaystyle{\delta \geqq 1}$のとき、 $\displaystyle{U_\delta(0)}$ は$\displaystyle{\mathbb{R}^2}$つまり全体になります。
もし余裕がありましたら、例えば関数上で定義された距離において、
開球はどんな形になるか考えてみるのもいいですね。
例えば$\displaystyle{d}$をユークリッド距離
$\displaystyle{d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}}$
とすれば、$\displaystyle{U_\delta(0)}$は原点中心の半径$\displaystyle{\delta}$の円になります。
もちろん「開球」の定義を見れば分かる通り、円周は含みませんが・・・

また$\displaystyle{d(x,y)=|x_1-y_1|+|x_2-y_2|}$ とすれば、$\displaystyle{U_\delta(0)}$はダイヤの形になります。

また$\displaystyle{d(x,y)=\max\{|x_1-y_1|,|x_2-y_2|\}}$ とすれば、$\displaystyle{U_\delta(0)}$は正方形になります。

次に$\displaystyle{d}$を自明な距離とすると(←自明な距離の説明はココ!)
$\displaystyle{\delta \lt 1}$のとき、 $\displaystyle{U_\delta(0)}$ は集合$\displaystyle{\{0\}}$つまり一つの元だけからなる集合になります。
$\displaystyle{\delta \geqq 1}$のとき、 $\displaystyle{U_\delta(0)}$ は$\displaystyle{\mathbb{R}^2}$つまり全体になります。
もし余裕がありましたら、例えば関数上で定義された距離において、
開球はどんな形になるか考えてみるのもいいですね。