距離とは?
Follow @tepika_math2点間の距離は?
さて、突然ですが、
以下の二つの点A、Bがあります。
点Aの座標は(3,4)で、
点Bの座標は(5,0)です。
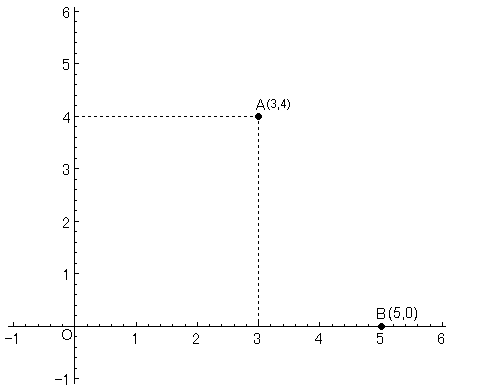
さて、
点Aと原点O間の距離と、
点Bと原点O間の距離はいつくになるでしょうか?
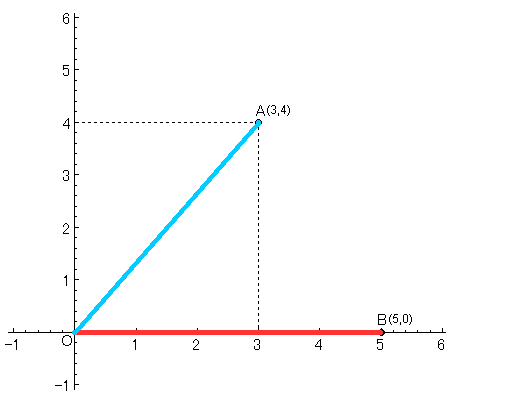
この距離は、中学の時に習った三平方の定理を使って解けますね?
点Aと原点O間の距離(図では青色の線)の長さは
$\displaystyle{\sqrt{3^2+4^2}=5}$ です。
また、点Bと原点Oの距離(図では赤色の線)の長さは5です。
つまり(図が悪い所は勘弁(_ _;))原点Oから点Aと点Bは同じ“距離”にあるといえます。
しかし・・・すこし制約を設けましょうか?
斜めには進めないとします。
つまり、縦と横にしか進めないとしたら、距離はいくらになるでしょうか?
(実際、京都の二条城のある町では、道路が交差していて縦と横にしか進めません。)
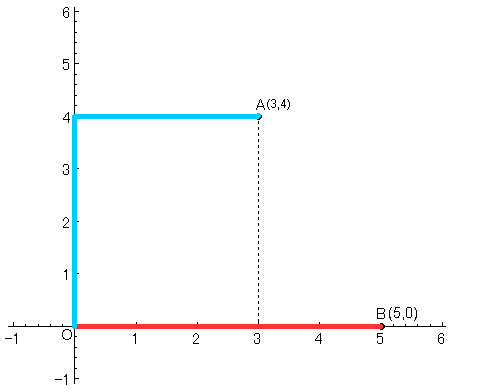
点Aと原点Oの距離は、上の図のように、
$\displaystyle{4+3=7}$
となりますが、
点Bと原点Oの距離は5のままです。
あれれ?
こっちの“距離”では点Aの方が点Bより遠くなってしまいますね?
このように、“距離”をどのように決めるかによって、
いろいろ何かが変わってきそうですね?
以下の二つの点A、Bがあります。
点Aの座標は(3,4)で、
点Bの座標は(5,0)です。
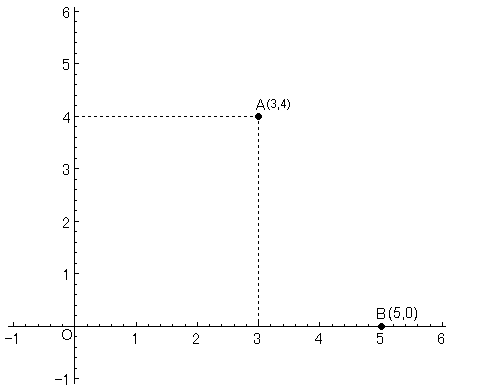
さて、
点Aと原点O間の距離と、
点Bと原点O間の距離はいつくになるでしょうか?

この距離は、中学の時に習った三平方の定理を使って解けますね?
点Aと原点O間の距離(図では青色の線)の長さは
$\displaystyle{\sqrt{3^2+4^2}=5}$ です。
また、点Bと原点Oの距離(図では赤色の線)の長さは5です。
つまり(図が悪い所は勘弁(_ _;))原点Oから点Aと点Bは同じ“距離”にあるといえます。
しかし・・・すこし制約を設けましょうか?
斜めには進めないとします。
つまり、縦と横にしか進めないとしたら、距離はいくらになるでしょうか?
(実際、京都の二条城のある町では、道路が交差していて縦と横にしか進めません。)

点Aと原点Oの距離は、上の図のように、
$\displaystyle{4+3=7}$
となりますが、
点Bと原点Oの距離は5のままです。
あれれ?
こっちの“距離”では点Aの方が点Bより遠くなってしまいますね?
このように、“距離”をどのように決めるかによって、
いろいろ何かが変わってきそうですね?
距離を抽象化しよう
はいっ!!!
ここでは、“距離”という概念を抽象化します。
$\displaystyle{\mathbb{X}}$ を集合とします。
写像 $\displaystyle{d:\mathbb{X}\times\mathbb{X} \rightarrow \mathbb{R}}$ が任意の$\displaystyle{\mathbb{X}}$の元a,b,cに対し、以下の性質をみたすとき、
$\displaystyle{d}$は$\displaystyle{\mathbb{X}}$上の距離であると言います。
[M1] $\displaystyle{d(a,b)\ge0}$かつ$\displaystyle{d(a,a)=0}$(正値性)
[M2] $\displaystyle{d(a,b)=d(b,a)}$(対称性)
[M3] $\displaystyle{d(a,c) \le d(a,b) + d(b,c)}$(三角不等式)
[M4] $\displaystyle{a \neq b}$ ならば $\displaystyle{d(a,b) \neq 0}$
[M1]では、距離の値は常にプラスの値となるということを表しています。
[M2]では、A地点からB地点までの距離と、B地点からA地点までの距離が同じことを表しています。
[M3]では、まぁ要するに回り道をするよりも、まっすぐ向かった方が近い、ということでしょうか?
[M4]では、違う点では絶対距離は0にはならない、ということを示しています。
つまり、このように定義すれば、何でも距離と呼びます。
例えば二次元平面の2点xとyの座標をそれぞれ
$\displaystyle{x=(x_1,x_2)}$
$\displaystyle{y=(y_1,y_2)}$
としてxとyの距離を
$\displaystyle{d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}}$
として定義するのもよし、
$\displaystyle{d(x,y)=|x_1-y_1|+|x_2-y_2|}$
として定義しても、
$\displaystyle{d(x,y)=\max\{|x_1-y_1|, |x_2-y_2|\}}$
も、
これらは上の[M1]〜[M4]を満たしているので、
これらは距離になります。
また、集合の元がひらがなでも国名でもよかったように(集合論でやりました)、
ひらがなや国名に距離も定義できちゃったりします。
ここでは、“距離”という概念を抽象化します。
$\displaystyle{\mathbb{X}}$ を集合とします。
写像 $\displaystyle{d:\mathbb{X}\times\mathbb{X} \rightarrow \mathbb{R}}$ が任意の$\displaystyle{\mathbb{X}}$の元a,b,cに対し、以下の性質をみたすとき、
$\displaystyle{d}$は$\displaystyle{\mathbb{X}}$上の距離であると言います。
[M1] $\displaystyle{d(a,b)\ge0}$かつ$\displaystyle{d(a,a)=0}$(正値性)
[M2] $\displaystyle{d(a,b)=d(b,a)}$(対称性)
[M3] $\displaystyle{d(a,c) \le d(a,b) + d(b,c)}$(三角不等式)
[M4] $\displaystyle{a \neq b}$ ならば $\displaystyle{d(a,b) \neq 0}$
[M1]では、距離の値は常にプラスの値となるということを表しています。
[M2]では、A地点からB地点までの距離と、B地点からA地点までの距離が同じことを表しています。
[M3]では、まぁ要するに回り道をするよりも、まっすぐ向かった方が近い、ということでしょうか?
[M4]では、違う点では絶対距離は0にはならない、ということを示しています。
つまり、このように定義すれば、何でも距離と呼びます。
例えば二次元平面の2点xとyの座標をそれぞれ
$\displaystyle{x=(x_1,x_2)}$
$\displaystyle{y=(y_1,y_2)}$
としてxとyの距離を
$\displaystyle{d(x,y)=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2}}$
として定義するのもよし、
$\displaystyle{d(x,y)=|x_1-y_1|+|x_2-y_2|}$
として定義しても、
$\displaystyle{d(x,y)=\max\{|x_1-y_1|, |x_2-y_2|\}}$
も、
これらは上の[M1]〜[M4]を満たしているので、
これらは距離になります。
また、集合の元がひらがなでも国名でもよかったように(集合論でやりました)、
ひらがなや国名に距離も定義できちゃったりします。