2つの開円が重なるとき、その共通部分は開集合になる
以下のように、開円Aと開円Bがあるとします。
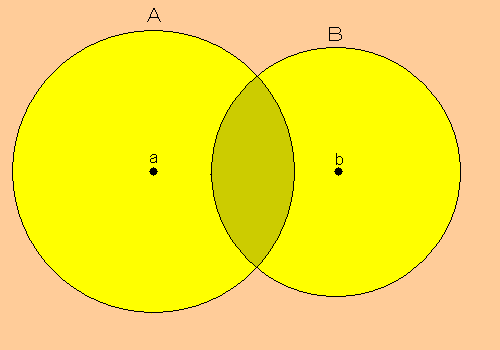
Aを中心の位置が$\displaystyle{a}$で、半径が$\displaystyle{r_a}$の円とし、
Bを中心の位置が$\displaystyle{b}$で、半径が$\displaystyle{r_b}$の円とします。
さて、以下のように開円Aと開円Bの重なる領域に、点cを任意にとります。
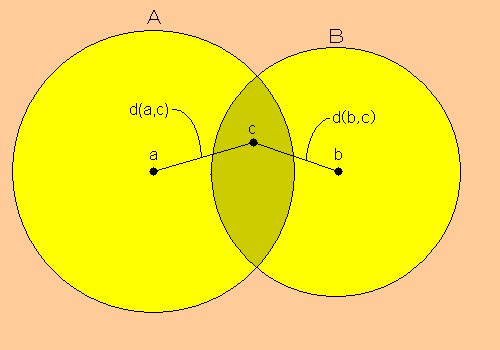
ただし、
$\displaystyle{d(a,c)}$は点$\displaystyle{a}$と点$\displaystyle{c}$の距離を、
$\displaystyle{d(b,c)}$は点$\displaystyle{b}$と点$\displaystyle{c}$の距離を表しています。
ここで、点$\displaystyle{c}$は、開円A内の点でもあり、同時に開円B内の点でもあるので、
$\displaystyle{d(a,c){\lt}r_a}$
$\displaystyle{d(b,c){\lt}r_b}$
の二つの不等式を同時に満たします。
ここで、
$\displaystyle{r_c=\min\{r_a-d(a,c),r_b-d(b,c)\}}$
とします。
ここで、$\displaystyle{r_c{\gt}0}$となっていることに注意しましょう。
ここで開円Cを、
中心が$\displaystyle{c}$で半径が$\displaystyle{r_c}$となるようにとると、
開円Cは図のように、開円Aと開円Bの重なっている領域に、すっぽり収まることになります。
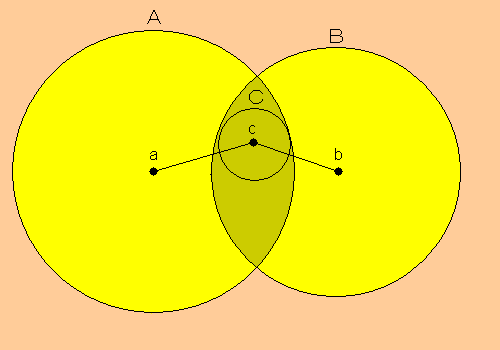
今から開円Cが、開円Aと開円Bの重なっている領域にきれいに収まることを示します。
たとえば、開円C内の任意の点$\displaystyle{d}$をとります。
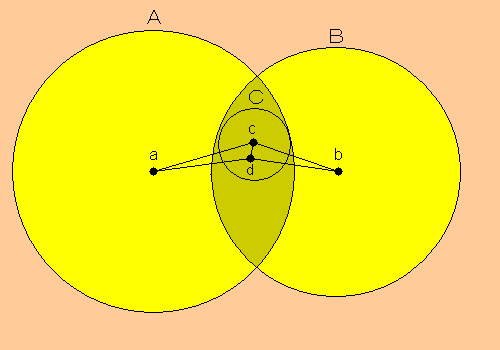
すると、
$\displaystyle{d(a,d)}$
$\displaystyle{{\leqq}d(a,c)+d(c,d)}$
$\displaystyle{{\lt}d(a,c)+r_c}$
$\displaystyle{{\leqq}d(a,c)+(r_a-d(a,c))}$
$\displaystyle{=r_a)}$
となります。
何だか複雑な式ですね・・・
それでは一行ずつ解説していきたいとおもいます。
1行目から2行目へは、三角不等式を使いました。
三角不等式の直感的な意味は、「寄り道するよりも、直接向かった方が近い」ということでしょうか・・・?
(三角不等式の詳しい解説は、また別のページで)
2行目から3行目は、
点$\displaystyle{d}$は、中心が$\displaystyle{c}$で半径$\displaystyle{r_c}$の開円内の点であることです。
3行目から4行目は、$\displaystyle{r_c}$の定義からです。
(∵min{a,b}≦a)
4行目から5行目は、括弧を外して普通に計算すれば求まります。
以上の式をまとめると、
$\displaystyle{d(a,d){\lt}r_a}$
となります。
ここで点$\displaystyle{d}$は、開円C内の任意の点です。
よって、開円内Cの任意の点は開円A内にあることが分かりました。
つまり開円Cは開円A内にすっぽり収まる、ということを意味しています。
同様に
$\displaystyle{d(b,d){\lt}r_b}$
も導き出されます。
これから、開円内Cの任意の点は開円B内にある、ということも分かり、
よって開円Cは、開円A内にも開円B内にも収まっている円ということになります。
結果、開円Cは開円Aと開円Bの重なる領域内に収まることが分かりました。
・・・以上のことより、2つの開円の共通部分の任意の点に対して、
その点を含む開円を、開円Aと開円Bの共通部分の中に収めることができるので、
2つの開円の共通部分の全ての点は内点になります。
よって、開集合になることが分かりました。

Aを中心の位置が$\displaystyle{a}$で、半径が$\displaystyle{r_a}$の円とし、
Bを中心の位置が$\displaystyle{b}$で、半径が$\displaystyle{r_b}$の円とします。
さて、以下のように開円Aと開円Bの重なる領域に、点cを任意にとります。

ただし、
$\displaystyle{d(a,c)}$は点$\displaystyle{a}$と点$\displaystyle{c}$の距離を、
$\displaystyle{d(b,c)}$は点$\displaystyle{b}$と点$\displaystyle{c}$の距離を表しています。
ここで、点$\displaystyle{c}$は、開円A内の点でもあり、同時に開円B内の点でもあるので、
$\displaystyle{d(a,c){\lt}r_a}$
$\displaystyle{d(b,c){\lt}r_b}$
の二つの不等式を同時に満たします。
ここで、
$\displaystyle{r_c=\min\{r_a-d(a,c),r_b-d(b,c)\}}$
とします。
ここで、$\displaystyle{r_c{\gt}0}$となっていることに注意しましょう。
ここで開円Cを、
中心が$\displaystyle{c}$で半径が$\displaystyle{r_c}$となるようにとると、
開円Cは図のように、開円Aと開円Bの重なっている領域に、すっぽり収まることになります。

今から開円Cが、開円Aと開円Bの重なっている領域にきれいに収まることを示します。
たとえば、開円C内の任意の点$\displaystyle{d}$をとります。

すると、
$\displaystyle{d(a,d)}$
$\displaystyle{{\leqq}d(a,c)+d(c,d)}$
$\displaystyle{{\lt}d(a,c)+r_c}$
$\displaystyle{{\leqq}d(a,c)+(r_a-d(a,c))}$
$\displaystyle{=r_a)}$
となります。
何だか複雑な式ですね・・・
それでは一行ずつ解説していきたいとおもいます。
1行目から2行目へは、三角不等式を使いました。
三角不等式の直感的な意味は、「寄り道するよりも、直接向かった方が近い」ということでしょうか・・・?
(三角不等式の詳しい解説は、また別のページで)
2行目から3行目は、
点$\displaystyle{d}$は、中心が$\displaystyle{c}$で半径$\displaystyle{r_c}$の開円内の点であることです。
3行目から4行目は、$\displaystyle{r_c}$の定義からです。
(∵min{a,b}≦a)
4行目から5行目は、括弧を外して普通に計算すれば求まります。
以上の式をまとめると、
$\displaystyle{d(a,d){\lt}r_a}$
となります。
ここで点$\displaystyle{d}$は、開円C内の任意の点です。
よって、開円内Cの任意の点は開円A内にあることが分かりました。
つまり開円Cは開円A内にすっぽり収まる、ということを意味しています。
同様に
$\displaystyle{d(b,d){\lt}r_b}$
も導き出されます。
これから、開円内Cの任意の点は開円B内にある、ということも分かり、
よって開円Cは、開円A内にも開円B内にも収まっている円ということになります。
結果、開円Cは開円Aと開円Bの重なる領域内に収まることが分かりました。
・・・以上のことより、2つの開円の共通部分の任意の点に対して、
その点を含む開円を、開円Aと開円Bの共通部分の中に収めることができるので、
2つの開円の共通部分の全ての点は内点になります。
よって、開集合になることが分かりました。