ベクトルの足し算
Follow @tepika_math同じ向きのベクトルの和
スカラー(ただの数のこと)では、足し算があったように、
ベクトルにも、足し算という概念があります。
一体、どうやって足し算をすればよいのでしょうか?
ベクトルの足し算は少しややこしいですが、がんばっていきましょう。
ベクトルの足し算には、
実は以下のような2通りの考え方があります。
まぁ、本ホームページでは、
1つ目を「A−タイプ」
2つ目を「B−タイプ」
とでもしましょうか(笑)
でも「A−タイプ」でも「B−タイプ」、どちらのやり方を選んでも、
結果として同じ答が出てきますので、
楽な方を選べばよいですね。
ベクトルにも、足し算という概念があります。
一体、どうやって足し算をすればよいのでしょうか?
ベクトルの足し算は少しややこしいですが、がんばっていきましょう。
ベクトルの足し算には、
実は以下のような2通りの考え方があります。
まぁ、本ホームページでは、
1つ目を「A−タイプ」
2つ目を「B−タイプ」
とでもしましょうか(笑)
でも「A−タイプ」でも「B−タイプ」、どちらのやり方を選んでも、
結果として同じ答が出てきますので、
楽な方を選べばよいですね。
A−タイプの考え方
例えば、以下の2つのベクトルの足し算を考えましょう。
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$???
$\displaystyle{=}$???
手順は以下の通りです☆
1.2つのベクトルの始点(矢印の最初の部分)、を揃えます。
2.そして、その2つのベクトルから、平行四辺形をつくります。
3.その平行四辺形の対角線上に、新しいベクトルを図のようにつくります。
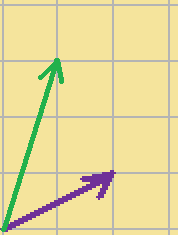
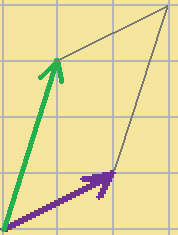
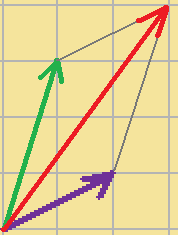
こうしてできた、上の赤いベクトルが、足し算の結果になります。
つまり、以下の通りです。
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$
$\displaystyle{=}$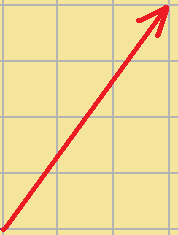
このように、平行四辺形を作図して、
ベクトルを求める方法があります。
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$???
$\displaystyle{=}$???手順は以下の通りです☆
1.2つのベクトルの始点(矢印の最初の部分)、を揃えます。
2.そして、その2つのベクトルから、平行四辺形をつくります。
3.その平行四辺形の対角線上に、新しいベクトルを図のようにつくります。



こうしてできた、上の赤いベクトルが、足し算の結果になります。
つまり、以下の通りです。
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$
$\displaystyle{=}$
このように、平行四辺形を作図して、
ベクトルを求める方法があります。
B−タイプの考え方
平行四辺形を作図する以外にも、
別の考え方もあります。
手順は以下の通りです☆
1.片方のベクトルの始点を、もう一方のベクトルの終点(矢印の先っぽ)に合わせます
2.そして、もう一方のベクトルの始点と、片方のベクトルの終点を結んだベクトルを作ります

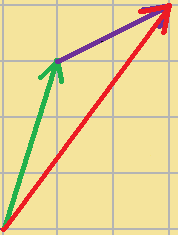
このようにベクトルの足し算は2通りの計算の仕方がありますが、
どちらのやり方も、結果として同じベクトルが出てきます。
別の考え方もあります。
手順は以下の通りです☆
1.片方のベクトルの始点を、もう一方のベクトルの終点(矢印の先っぽ)に合わせます
2.そして、もう一方のベクトルの始点と、片方のベクトルの終点を結んだベクトルを作ります


このようにベクトルの足し算は2通りの計算の仕方がありますが、
どちらのやり方も、結果として同じベクトルが出てきます。
同じ向きのときは!?
ベクトルの足し算には、以上の2通りの考え方があります。
それでわ、
 $\displaystyle{+}$
$\displaystyle{+}$
みたいに、同じ向きの場合はどうなるでしょうか?
A−タイプみたいに、平行四辺形を作っても、つぶれちゃいますね。
でもB−タイプでやったら、分かると思います。
片方のベクトルの始点に、もう一方のベクトルの終点を合わせますと、

になるので、
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$
$\displaystyle{=}$
となります。
それでわ、
 $\displaystyle{+}$
$\displaystyle{+}$
みたいに、同じ向きの場合はどうなるでしょうか?
A−タイプみたいに、平行四辺形を作っても、つぶれちゃいますね。
でもB−タイプでやったら、分かると思います。
片方のベクトルの始点に、もう一方のベクトルの終点を合わせますと、

になるので、
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$
$\displaystyle{=}$
となります。
正反対のときは!?
 $\displaystyle{+}$
$\displaystyle{+}$
のときも、A−タイプのやり方でやると、平行四辺形がつぶれます。
だからこの場合も、B−タイプのやり方がよさそうですね。

になるので、
 $\displaystyle{+}$
$\displaystyle{+}$ $\displaystyle{=}$
$\displaystyle{=}$
になります。
ゼロベクトル
前回、ゼロベクトルのことを紹介しました。
ゼロベクトルは、長さが0のベクトルです。
だから、どんなベクトルにゼロベクトルを足しても、そのままです。
これは、どんな数に0を足しても、変わらないというのと同じですね。
$\displaystyle{\vec{a}+\vec{0}=\vec{a}}$
$\displaystyle{\vec{0}+\vec{a}=\vec{a}}$
です。
ゼロベクトルは、長さが0のベクトルです。
だから、どんなベクトルにゼロベクトルを足しても、そのままです。
これは、どんな数に0を足しても、変わらないというのと同じですね。
$\displaystyle{\vec{a}+\vec{0}=\vec{a}}$
$\displaystyle{\vec{0}+\vec{a}=\vec{a}}$
です。