成分表示によるベクトルの演算
Follow @tepika_mathベクトルの成分表示を使うと・・・
前回は、ベクトルを矢印の代わりに成分表示で表わす、とういことを表しました。
以前にベクトルの足し算・引き算・内積を説明しましたが、
それらの計算もベクトルの成分表示を使うと、簡単に計算できちゃいます☆ミ
今回は、成分表示によるベクトル計算を紹介したいと思います。
以前にベクトルの足し算・引き算・内積を説明しましたが、
それらの計算もベクトルの成分表示を使うと、簡単に計算できちゃいます☆ミ
今回は、成分表示によるベクトル計算を紹介したいと思います。
足し算
以下の2つのベクトルがあるとします。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
このとき、上の2つのベクトルの足し算を求めるには、
各成分ごとに足していけばいいのです。
つまり、
$\displaystyle{\vec{a}+\vec{b}}$
$\displaystyle{=(k,l)+(m,n)}$
$\displaystyle{=(k+m,l+n)}$
となります。
例えば、以下の例をみてみます。
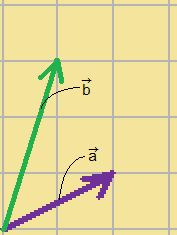
見て分かる通り、
$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
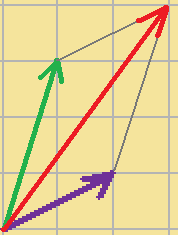
この2つのベクトルの和
$\displaystyle{\vec{a}+\vec{b}}$
を求めるとき、
わざわざ平行四辺形をつくり・・・大変でしょうか?
でもベクトルの足し算を成分表示を使い計算すると、
$\displaystyle{\vec{a}+\vec{b}}$
$\displaystyle{=(2,1)+(1,3)}$
$\displaystyle{=(2+1,1+3)}$
$\displaystyle{=(3,4)}$
です。
実際に平行四辺形を作って求めるベクトルと値が一致していることを確認してみるとよいでしょう。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
このとき、上の2つのベクトルの足し算を求めるには、
各成分ごとに足していけばいいのです。
つまり、
$\displaystyle{\vec{a}+\vec{b}}$
$\displaystyle{=(k,l)+(m,n)}$
$\displaystyle{=(k+m,l+n)}$
となります。
例えば、以下の例をみてみます。

見て分かる通り、
$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
この2つのベクトルの和
$\displaystyle{\vec{a}+\vec{b}}$
を求めるとき、
わざわざ平行四辺形をつくり・・・大変でしょうか?
でもベクトルの足し算を成分表示を使い計算すると、
$\displaystyle{\vec{a}+\vec{b}}$
$\displaystyle{=(2,1)+(1,3)}$
$\displaystyle{=(2+1,1+3)}$
$\displaystyle{=(3,4)}$
です。
実際に平行四辺形を作って求めるベクトルと値が一致していることを確認してみるとよいでしょう。

引き算
引き算も、足し算と似ています。
以下の2つのベクトルがあるとします。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
このとき、上の2つのベクトルの引き算を求めるには、
各成分ごとに足していけばいいのです。
つまり、
$\displaystyle{\vec{a}-\vec{b}}$
$\displaystyle{=(k,l)-(m,n)}$
$\displaystyle{=(k-m,l-n)}$
となります。
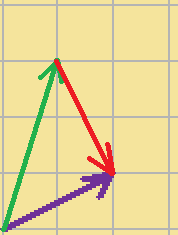
例えば、以下の例をみてみます。

見て分かる通り、
$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
この2つのベクトルの差
$\displaystyle{\vec{a}-\vec{b}}$
を求めましょう。
$\displaystyle{\vec{a}-\vec{b}}$
$\displaystyle{=(2,1)-(1,3)}$
$\displaystyle{=(2-1,1-3)}$
$\displaystyle{=(1,-2)}$
です。
以下の2つのベクトルがあるとします。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
このとき、上の2つのベクトルの引き算を求めるには、
各成分ごとに足していけばいいのです。
つまり、
$\displaystyle{\vec{a}-\vec{b}}$
$\displaystyle{=(k,l)-(m,n)}$
$\displaystyle{=(k-m,l-n)}$
となります。
例えば、以下の例をみてみます。

見て分かる通り、
$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
この2つのベクトルの差
$\displaystyle{\vec{a}-\vec{b}}$
を求めましょう。
$\displaystyle{\vec{a}-\vec{b}}$
$\displaystyle{=(2,1)-(1,3)}$
$\displaystyle{=(2-1,1-3)}$
$\displaystyle{=(1,-2)}$
です。

内積
内積は、たしかめんどくさかったですね?
ベクトルの長さを求め、
それから2つのベクトルのなす角度$\displaystyle{\theta}$を求めて、その $\displaystyle{\cos\theta}$
でも成分表示を使った方が、一層簡単になります。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
この2つのベクトルの内積は、
$\displaystyle{\vec{a}\cdot\vec{b}}$
$\displaystyle{=(k,l)\cdot(m,n)}$
$\displaystyle{=km+ln}$
です。
以下のとき、

$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
この2つのベクトルの内積は
$\displaystyle{\vec{a}\cdot\vec{b}}$
$\displaystyle{(2,1)\cdot(1,3)}$
$\displaystyle{2\times1+1\times3=5}$
です。
このように、成分表示を使えば、
2つのベクトルのなす角度$\displaystyle{\theta}$を求めなくても、
内積が計算できます。
ベクトルの長さを求め、
それから2つのベクトルのなす角度$\displaystyle{\theta}$を求めて、その $\displaystyle{\cos\theta}$
でも成分表示を使った方が、一層簡単になります。
$\displaystyle{\vec{a}=(k,l)}$
$\displaystyle{\vec{b}=(m,n)}$
この2つのベクトルの内積は、
$\displaystyle{\vec{a}\cdot\vec{b}}$
$\displaystyle{=(k,l)\cdot(m,n)}$
$\displaystyle{=km+ln}$
です。
以下のとき、

$\displaystyle{\vec{a}=(2,1)}$
$\displaystyle{\vec{b}=(1,3)}$
です。
この2つのベクトルの内積は
$\displaystyle{\vec{a}\cdot\vec{b}}$
$\displaystyle{(2,1)\cdot(1,3)}$
$\displaystyle{2\times1+1\times3=5}$
です。
このように、成分表示を使えば、
2つのベクトルのなす角度$\displaystyle{\theta}$を求めなくても、
内積が計算できます。