内積
Follow @tepika_math内積って?
ではでは(^ ^)ノシ
ベクトルの掛け算(?)とも言われている、
内積というものについて、解説したいと思います。
つまり、ベクトルに和と差の概念があるように、積みたいな概念が存在します。それを「内積」と呼ぶのです!
ところで普通の数の場合、掛け算は$\displaystyle{\times}$か$\displaystyle{\cdot}$という記号を使いましたが、
ベクトルの内積では$\displaystyle{\cdot}$の方を使います。
だからベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$の内積は
$\displaystyle{\vec{a}\cdot\vec{b}}$
と書かれます。
決して↓↓
$\displaystyle{\vec{a}\times\vec{b}}$
と書かないように・・・
ベクトルの掛け算(?)とも言われている、
内積というものについて、解説したいと思います。
つまり、ベクトルに和と差の概念があるように、積みたいな概念が存在します。それを「内積」と呼ぶのです!
ところで普通の数の場合、掛け算は$\displaystyle{\times}$か$\displaystyle{\cdot}$という記号を使いましたが、
ベクトルの内積では$\displaystyle{\cdot}$の方を使います。
だからベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$の内積は
$\displaystyle{\vec{a}\cdot\vec{b}}$
と書かれます。
決して↓↓
$\displaystyle{\vec{a}\times\vec{b}}$
と書かないように・・・
内積の定義
それでは、「内積」とは、一体何なのかを具体的に説明しましょう。
以下のように、ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ のなす角を$\displaystyle{\theta}$とします。
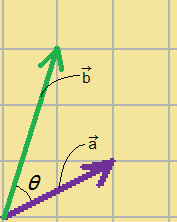
ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ の内積$\displaystyle{\vec{a}\cdot\vec{b}}$は
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta}$
とします。
ところで、上の図より
$\displaystyle{|\vec{a}|=\sqrt{5}}$
$\displaystyle{|\vec{b}|=\sqrt{10}}$
となることが分かると思うので(三平方の定理を使ってください)、
よってこのときは
$\displaystyle{\vec{a}\cdot\vec{b}=\sqrt{5}\times\sqrt{10}}$
$\displaystyle{=5\sqrt{2}\cos\theta}$
となります。
以下のように、ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ のなす角を$\displaystyle{\theta}$とします。

ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ の内積$\displaystyle{\vec{a}\cdot\vec{b}}$は
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta}$
とします。
ところで、上の図より
$\displaystyle{|\vec{a}|=\sqrt{5}}$
$\displaystyle{|\vec{b}|=\sqrt{10}}$
となることが分かると思うので(三平方の定理を使ってください)、
よってこのときは
$\displaystyle{\vec{a}\cdot\vec{b}=\sqrt{5}\times\sqrt{10}}$
$\displaystyle{=5\sqrt{2}\cos\theta}$
となります。
内積について
内積は理解できたでしょうか?
内積を求めるには、まず2つのベクトルのなす角を調べてから、cosを計算しなければなりません。
結構大変でしょうか?
ところで、重要なことがあります!!!
ベクトルの内積は、実はスカラー、つまりただの数になるのです。
繰り返しますが、ベクトルとベクトルの内積は、ベクトルじゃありません。
もはや、方向を持たない、ただの数になります。
最初は、「なんだ、そんなことか・・・」とか思うかもしれませんが、
結構重要なことなので。。。
内積を求めるには、まず2つのベクトルのなす角を調べてから、cosを計算しなければなりません。
結構大変でしょうか?
ところで、重要なことがあります!!!
ベクトルの内積は、実はスカラー、つまりただの数になるのです。
繰り返しますが、ベクトルとベクトルの内積は、ベクトルじゃありません。
もはや、方向を持たない、ただの数になります。
最初は、「なんだ、そんなことか・・・」とか思うかもしれませんが、
結構重要なことなので。。。