内積の性質
Follow @tepika_math直交
内積は大丈夫ですか?
ところで、
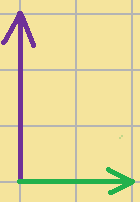
のように、ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ が垂直に交わっている場合はどうなるでしょう?
垂直なので、
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos90^\circ}$
となりますが、
ところで、
$\displaystyle{\cos90^\circ=0}$です。
だから結局、
$\displaystyle{\vec{a}\cdot\vec{b}=0}$
となります。
つまりベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$が垂直に交わっている(直交している)ときは、2つのベクトルの内積は容赦なく0になります。
逆にいえば、2つのベクトルの内積が0になっていたら、
この2つのベクトルは直交していることが言えます。
ところで、

のように、ベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$ が垂直に交わっている場合はどうなるでしょう?
垂直なので、
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos90^\circ}$
となりますが、
ところで、
$\displaystyle{\cos90^\circ=0}$です。
だから結局、
$\displaystyle{\vec{a}\cdot\vec{b}=0}$
となります。
つまりベクトル$\displaystyle{\vec{a}}$とベクトル$\displaystyle{\vec{b}}$が垂直に交わっている(直交している)ときは、2つのベクトルの内積は容赦なく0になります。
逆にいえば、2つのベクトルの内積が0になっていたら、
この2つのベクトルは直交していることが言えます。
内積に関する公式
内積は分かりましたか?
それでは、以下に内積のいくつかの公式を挙げたいと思います。
それでは、以下に内積のいくつかの公式を挙げたいと思います。
- $\displaystyle{\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}}$(分配法則)
- $\displaystyle{\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}}$(交換法則)
- $\displaystyle{k\vec{a}\cdot\vec{b}=(k\vec{a})\cdot\vec{b}=\vec{a}\cdot(k\vec{b})}$(スカラー倍。ただし$\displaystyle{k}$は定数)