ベクトルと物理学の関係
Follow @tepika_math単位
その前に・・・
物理には、いろいろな単位が出てきます。
質量・速度・温度・etc...
しかし、その「単位」も、実は2グループに分かれるのです。
何だかあるなしクイズみたいですね☆・・・ぢゃなくて、、、
以上のように物理に出てくる「単位」は2種類に分かれますが・・・
この2種類の単位の違い、さっぱり分らない人はいませんか!!!??
もし「さっぱり分らない」ってな人は、物理では泣きを見ることになりますよ〜(T_T)
物理には、いろいろな単位が出てきます。
質量・速度・温度・etc...
しかし、その「単位」も、実は2グループに分かれるのです。
| グループA | グループB |
|---|---|
|
時間(s) 質量(kg) 温度(℃) エネルギー(J) |
速度(m/s) 加速度(m/s2) 力(N) 運動量・力積(kg・m/s or N・s) |
以上のように物理に出てくる「単位」は2種類に分かれますが・・・
この2種類の単位の違い、さっぱり分らない人はいませんか!!!??
もし「さっぱり分らない」ってな人は、物理では泣きを見ることになりますよ〜(T_T)
2つの単位の違い
「じゃぁ、一体どのように違うの〜??」とお思いの方は、これから説明します。
例えば、現在の気温が20℃だとします。
20℃にまた3℃だけ加わったら何℃になりますか?
23℃Kですね。・・・こんなのあたりまえですね。
それでは、今度は力です。
ある物体Aに3Nの力が加わっているとします。
それにまた3Nの力を加えたら、どうなるでしょうか?
3N+3N=6N?
実は、そうにはならないことがあります。
例えば、現在の気温が20℃だとします。
20℃にまた3℃だけ加わったら何℃になりますか?
23℃Kですね。・・・こんなのあたりまえですね。
それでは、今度は力です。
ある物体Aに3Nの力が加わっているとします。
それにまた3Nの力を加えたら、どうなるでしょうか?
3N+3N=6N?
実は、そうにはならないことがあります。
力の向き
以下のように3Nの力が2つ働いているとしたら・・・?
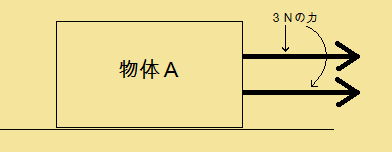
この場合でしたら、容赦なく力は
3N+3N=6Nになりますね。
しかし、以下のような場合を考えてください。

このように反対向きに力が働いている場合、どうなるでしょうか?
この場合、力のつりあっているので、
働いている力の合計はゼロNになります。
3Nに、さらに3Nの力を加えたらゼロNになってしまった!!
こんなことが起こります。

この場合でしたら、容赦なく力は
3N+3N=6Nになりますね。
しかし、以下のような場合を考えてください。

このように反対向きに力が働いている場合、どうなるでしょうか?
この場合、力のつりあっているので、
働いている力の合計はゼロNになります。
3Nに、さらに3Nの力を加えたらゼロNになってしまった!!
こんなことが起こります。
力はベクトルだった
このように、3Nの力が働いている物体に、
また3Nの力を加えても、
加える方向によっては力が6NにもなったりゼロNにもなったりします。
「方向によって違う・・・」
・・・これは、ベクトルです!
力とはベクトルだったのです。
ベクトルの足し算は、ただ大きさを足すのではなく、
確か平行四辺形を作って求めるのでしたね?
(確かに力の合力は平行四辺形を作って求めましたね?これはベクトルの演算です。合力は・・・高校物理の教科書でも読んでください)
大きさが3である2つのベクトルを足したベクトルの大きさが、
6になるとは限りませんからね。
つまり、
グループA・・・スカラー
グループB・・・ベクトル
と考えられます。
私たちが日常使っている単位でも、
ベクトルとスカラーの2種類があるとは、驚きですね。
また3Nの力を加えても、
加える方向によっては力が6NにもなったりゼロNにもなったりします。
「方向によって違う・・・」
・・・これは、ベクトルです!
力とはベクトルだったのです。
ベクトルの足し算は、ただ大きさを足すのではなく、
確か平行四辺形を作って求めるのでしたね?
(確かに力の合力は平行四辺形を作って求めましたね?これはベクトルの演算です。合力は・・・高校物理の教科書でも読んでください)
大きさが3である2つのベクトルを足したベクトルの大きさが、
6になるとは限りませんからね。
つまり、
グループA・・・スカラー
グループB・・・ベクトル
と考えられます。
私たちが日常使っている単位でも、
ベクトルとスカラーの2種類があるとは、驚きですね。
ボールの跳ね返り
さて、以下のように、
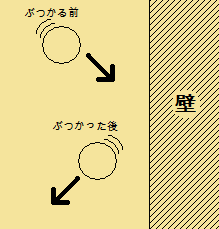
3m/sで進んでいるボールが壁に当たり、
跳ね返って再び3m/sで進むとします。
さて、ボールが跳ね返る前と跳ね返った後・・・ボールの速度は変化したでしょうか?
「跳ね返った後も3m/sだから、速度は変わらないんじゃ・・・?」
・・・と少しでも思った方いるでしょうか。いや、違うよ。
結論からいえば、ボールの速度は変化しました。
よく考えてください。
速度はベクトルです。
ベクトルは大きさが同じでも
向きが違えば違うベクトルとみなします。
このとき、「速度の大きさ」は同じでも「速度の向き」が違うので、
跳ね返る前と跳ね返った後は速度は変化したことになります。
・・・ところで、物理において「速度」と「速さ」は違う言葉としてみなし、区別します。
「速度」とは、ベクトルとして見なしますが、
「速さ」はスカラーと見なします。
「速度」というベクトルの大きさは「速さ」と呼ばれます。
もし「速さ」だったら、跳ね返り前と後で変化しないですが・・・
ところで日常用語では「速度」と「速さ」を同じ意味の言葉として扱い、区別しません。
ここでも、日常用語と物理用語のギャップがありますね。

3m/sで進んでいるボールが壁に当たり、
跳ね返って再び3m/sで進むとします。
さて、ボールが跳ね返る前と跳ね返った後・・・ボールの速度は変化したでしょうか?
「跳ね返った後も3m/sだから、速度は変わらないんじゃ・・・?」
・・・と少しでも思った方いるでしょうか。いや、違うよ。
結論からいえば、ボールの速度は変化しました。
よく考えてください。
速度はベクトルです。
ベクトルは大きさが同じでも
向きが違えば違うベクトルとみなします。
このとき、「速度の大きさ」は同じでも「速度の向き」が違うので、
跳ね返る前と跳ね返った後は速度は変化したことになります。
・・・ところで、物理において「速度」と「速さ」は違う言葉としてみなし、区別します。
「速度」とは、ベクトルとして見なしますが、
「速さ」はスカラーと見なします。
「速度」というベクトルの大きさは「速さ」と呼ばれます。
もし「速さ」だったら、跳ね返り前と後で変化しないですが・・・
ところで日常用語では「速度」と「速さ」を同じ意味の言葉として扱い、区別しません。
ここでも、日常用語と物理用語のギャップがありますね。
等速円運動
次は、ある物体が以下の図のようにくるくる回っているとします。(できたら観覧車を書きたかった・・・絵が下手だなぁと思う)
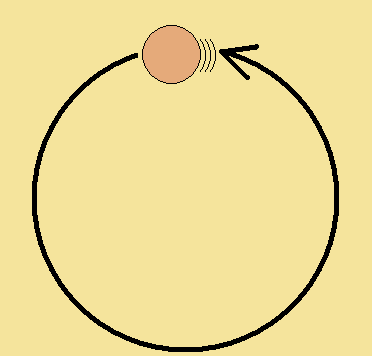
同じ“速さ”で回っているとします。
さて“速度”は変化したでしょうか?
上と同じです。“速度”はベクトルなので、速度は常に変化しています。
向きが変化していますからね。
ところで、速度が常に変化している、ということは力が働いています。
もし力が働いていなかったら、等速直線運動するはずです(以下を参照)
それでは、この回っている物体には、どの向きに働いているのでしょうか?
・・・答えは中心向きです。
力が常に中心を向くとき、物体はくるくると円運動をします。
身近な例が・・・惑星や月ですかね?
惑星と太陽の間(または地球と月の間)には重力が働いています。
だから、中心向きに力が働いている、ということで、ぐるぐる回っているのですね?

同じ“速さ”で回っているとします。
さて“速度”は変化したでしょうか?
上と同じです。“速度”はベクトルなので、速度は常に変化しています。
向きが変化していますからね。
ところで、速度が常に変化している、ということは力が働いています。
もし力が働いていなかったら、等速直線運動するはずです(以下を参照)
それでは、この回っている物体には、どの向きに働いているのでしょうか?
・・・答えは中心向きです。
力が常に中心を向くとき、物体はくるくると円運動をします。
身近な例が・・・惑星や月ですかね?
惑星と太陽の間(または地球と月の間)には重力が働いています。
だから、中心向きに力が働いている、ということで、ぐるぐる回っているのですね?
運動方程式F=maを正しく解釈しよう
少し余談ですが・・・
「物体に力を加えたら、物体は動くんだよね?」
とか
「物体に力を加えなかったら、物体は止まるんだよね?」
と考えている人はいませんか!?
この考え方は物理を、できなくしてしまいます。
これからの議論は、少々ややこしいので、何回も繰り返しよむことをオススメします☆
まず運動方程式を思い出してください。(高校の時にやったかな?)
$\displaystyle{F}$を力、 $\displaystyle{m}$を質量、 $\displaystyle{a}$を加速度として
$\displaystyle{F=ma}$
が成り立ちます。
これをみて分かるように、力と加速度は密接な関係にあり、
切っても切っても切り離せない絆で結ばれています。
加速度の働いていない物体は力なんて働いていません。
同様に力がなければ加速度なんておこりません。
※ちなみに、速度の単位は(m/s)で加速度の単位は(m/s2)です。
例えば3m/sは一秒間に3m進む速度のことをしめしていて、
3m/s2は一秒間に3m/s速度が増える加速度を示しています。
・・・とここで疑問に思うかもしれませんが。
「私たちは地球にいる限り重力という“力”が働いているのに、ちゃんと止まることができるよ!?」
確かに、そこらに落ちている石にも、重力が働いていますが・・・止まってますね。全然加速度運動してませんよね?
ということは、石に働いている力は結局ゼロNなのです。
何がゼロNかって??そう、合力が!!!
確かに石には重力は働いていますが、地面に接触している限り、垂直抗力という力が働き、
結局重力と垂直抗力が働き、つりあってゼロNになります。
確かに垂直抗力を外す(例えば地面に接触していないとき)は、重力だけが働き、加速度運動します。
運動方程式F=maだけで見ると、
「力が全く働いていない」であるのと「力は働いているが、つりあって力の合力がゼロN」は全く等価です。
なぜなら、物理でいう“力”とは、加速度を生じさせるモノなのです。
これも日常での“力”と物理での“力”の違いなのでしょうか?
合力がゼロでないときは、加速度運動をするのです。
さてさて、力が働いているときは、加速度運動をするのでした。
それでは力が働いていない時は・・・?
運動方程式から分かるように、加速度は0になります。
つまり、「止まる??」ぢゃなくて、「等速直線運動」をします。
ところで、「静止状態」もアリです。
なぜなら「静止状態」も、速度が0の等速直線運動と考えられます。
だから、力を加えなければ、
止まっている物体は止まったままだし、
動いている物体はそのままの速度で動き続けます(これを慣性の法則といいます)
でも・・・?(・_・;)
確かに物体を転がしたら、しだいに減速していって、いずれかは止まってしまいますが・・・
これは、動く物体には「摩擦力」という力が働いているためです。
摩擦力が働くから、物体が加速度運動するのです。
「あれ・・・加速度運動?減速してるのに?」
と思うかもしれませんが、「減速」も「大きさがマイナスの加速度運動」と考えます。
ところで、「マイナスの加速度」とか、けっこう曖昧ですね?
・・・何が?と思うかもしれませんが、
以下の図のように
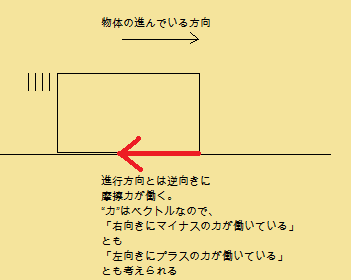
右にマイナスの力が働いているとも考えられるし、左にプラスの力が働いていると考えてもいいわけです。
ただ符号の違いだけですが・・・
でも普通は正になるベクトルの向きを基準に考えます。
この場合、左に力が働いていると考えると力は正になるので、力の向きは左と考えるわけです。
まぁ要するに、力を加えなかったら、等速直線運動する、ということです。
くれぐれも、 $\displaystyle{v}$を速度として
$\displaystyle{F=mv}$
としてはいけませんよ。
力がなくても、物体は動きます。
ボールを横にチョンと転がしたとき、手を離してもボールは確かに少し動き続けますが、
「それは力が残っていて、その力で横に動いているんだよね?」
そんなことは、絶対にありませんっ!!!!!
そもそも力は、物体と物体が接触しなければ働きません。
物体を押す時、手で押すとか何かして、確かに物体に触れているでしょ?
離れいても働く力は、
でもなきゃ、超能力だよ、ホント。。。
「物体に力を加えたら、物体は動くんだよね?」
とか
「物体に力を加えなかったら、物体は止まるんだよね?」
と考えている人はいませんか!?
この考え方は物理を、できなくしてしまいます。
これからの議論は、少々ややこしいので、何回も繰り返しよむことをオススメします☆
まず運動方程式を思い出してください。(高校の時にやったかな?)
$\displaystyle{F}$を力、 $\displaystyle{m}$を質量、 $\displaystyle{a}$を加速度として
$\displaystyle{F=ma}$
が成り立ちます。
これをみて分かるように、力と加速度は密接な関係にあり、
切っても切っても切り離せない絆で結ばれています。
加速度の働いていない物体は力なんて働いていません。
同様に力がなければ加速度なんておこりません。
※ちなみに、速度の単位は(m/s)で加速度の単位は(m/s2)です。
例えば3m/sは一秒間に3m進む速度のことをしめしていて、
3m/s2は一秒間に3m/s速度が増える加速度を示しています。
・・・とここで疑問に思うかもしれませんが。
「私たちは地球にいる限り重力という“力”が働いているのに、ちゃんと止まることができるよ!?」
確かに、そこらに落ちている石にも、重力が働いていますが・・・止まってますね。全然加速度運動してませんよね?
ということは、石に働いている力は結局ゼロNなのです。
何がゼロNかって??そう、合力が!!!
確かに石には重力は働いていますが、地面に接触している限り、垂直抗力という力が働き、
結局重力と垂直抗力が働き、つりあってゼロNになります。
確かに垂直抗力を外す(例えば地面に接触していないとき)は、重力だけが働き、加速度運動します。
運動方程式F=maだけで見ると、
「力が全く働いていない」であるのと「力は働いているが、つりあって力の合力がゼロN」は全く等価です。
なぜなら、物理でいう“力”とは、加速度を生じさせるモノなのです。
これも日常での“力”と物理での“力”の違いなのでしょうか?
合力がゼロでないときは、加速度運動をするのです。
さてさて、力が働いているときは、加速度運動をするのでした。
それでは力が働いていない時は・・・?
運動方程式から分かるように、加速度は0になります。
つまり、「止まる??」ぢゃなくて、「等速直線運動」をします。
ところで、「静止状態」もアリです。
なぜなら「静止状態」も、速度が0の等速直線運動と考えられます。
だから、力を加えなければ、
止まっている物体は止まったままだし、
動いている物体はそのままの速度で動き続けます(これを慣性の法則といいます)
でも・・・?(・_・;)
確かに物体を転がしたら、しだいに減速していって、いずれかは止まってしまいますが・・・
これは、動く物体には「摩擦力」という力が働いているためです。
摩擦力が働くから、物体が加速度運動するのです。
「あれ・・・加速度運動?減速してるのに?」
と思うかもしれませんが、「減速」も「大きさがマイナスの加速度運動」と考えます。
ところで、「マイナスの加速度」とか、けっこう曖昧ですね?
・・・何が?と思うかもしれませんが、
以下の図のように

右にマイナスの力が働いているとも考えられるし、左にプラスの力が働いていると考えてもいいわけです。
ただ符号の違いだけですが・・・
でも普通は正になるベクトルの向きを基準に考えます。
この場合、左に力が働いていると考えると力は正になるので、力の向きは左と考えるわけです。
まぁ要するに、力を加えなかったら、等速直線運動する、ということです。
くれぐれも、 $\displaystyle{v}$を速度として
$\displaystyle{F=mv}$
としてはいけませんよ。
力がなくても、物体は動きます。
ボールを横にチョンと転がしたとき、手を離してもボールは確かに少し動き続けますが、
「それは力が残っていて、その力で横に動いているんだよね?」
そんなことは、絶対にありませんっ!!!!!
そもそも力は、物体と物体が接触しなければ働きません。
物体を押す時、手で押すとか何かして、確かに物体に触れているでしょ?
離れいても働く力は、
- 重力
- 磁石の力
- 静電気の力
でもなきゃ、超能力だよ、ホント。。。
遠心力の秘密
電車の中で、ボールを真上に投げても、結局は元の位置に落ちます。
電車の中で投げたボールが後ろに置いてかれることはありませんね?
それはボールも電車とともに等速度運動をしているからです。
しかし、加速度運動している電車ではどうなるか・・・?
もし電車が加速度運動しているとしたら、今度は電車の中の人は加速度の向きと逆向きに置いてかれます。
だから、真上に投げたボールも後ろに置いてかれます。
日常でもこの現象はよく見られます。
例えば電車が急停車するとき、
減速、つまり進行方向と逆向きに加速度がはたらくわけなので、
進行方向の逆向きの逆向き・・・まぁ進行方向に体が倒れてしまうわけです。
電車がぐんぐん速くなっているときも、同様です。
ところで、円運動している物体は、中心向きに力が働いているのでしたね?
それはつまり、中心向きに加速度が働いていることになります。
だから、円運動している物体の中にいる人には、円の外側に力が働いているように感じます。
それが、いわゆる“遠心力”と呼ばれるものです。
ところで、このときの力を「慣性力」あるいは「見かけの力」といいます。
「見かけの力」という名前の通り、本当に見かけの力なのです。
見かけの力ぁ・・・?
あんまり、イメージつきにくいですね?
こーゆーときは、とりあえず「スーパーマリオブラザーズ」の世界を思い浮かべましょう(笑)
マリオの世界はすごいです。ブロックが中に浮いているんですもの。一体どんな原理なのでしょうか?
まぁ、それは置いといて、とりあえずブロックが電車の中にあるとして、
一方ブロックが地面に対して静止しているとします。
さて、以下の図を見てください。
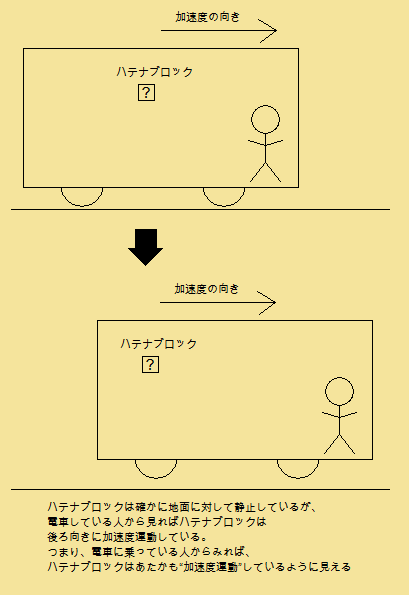
こうしてみると、加速度運動している電車の中では、
地面に対して止まっている物体が、
あたかも加速度を受けているように見えてしまいます。
これが、見かけの力です!!!
電車の中で投げたボールが後ろに置いてかれることはありませんね?
それはボールも電車とともに等速度運動をしているからです。
しかし、加速度運動している電車ではどうなるか・・・?
もし電車が加速度運動しているとしたら、今度は電車の中の人は加速度の向きと逆向きに置いてかれます。
だから、真上に投げたボールも後ろに置いてかれます。
日常でもこの現象はよく見られます。
例えば電車が急停車するとき、
減速、つまり進行方向と逆向きに加速度がはたらくわけなので、
進行方向の逆向きの逆向き・・・まぁ進行方向に体が倒れてしまうわけです。
電車がぐんぐん速くなっているときも、同様です。
ところで、円運動している物体は、中心向きに力が働いているのでしたね?
それはつまり、中心向きに加速度が働いていることになります。
だから、円運動している物体の中にいる人には、円の外側に力が働いているように感じます。
それが、いわゆる“遠心力”と呼ばれるものです。
ところで、このときの力を「慣性力」あるいは「見かけの力」といいます。
「見かけの力」という名前の通り、本当に見かけの力なのです。
見かけの力ぁ・・・?
あんまり、イメージつきにくいですね?
こーゆーときは、とりあえず「スーパーマリオブラザーズ」の世界を思い浮かべましょう(笑)
マリオの世界はすごいです。ブロックが中に浮いているんですもの。一体どんな原理なのでしょうか?
まぁ、それは置いといて、とりあえずブロックが電車の中にあるとして、
一方ブロックが地面に対して静止しているとします。
さて、以下の図を見てください。

こうしてみると、加速度運動している電車の中では、
地面に対して止まっている物体が、
あたかも加速度を受けているように見えてしまいます。
これが、見かけの力です!!!
仕事とは?
さて、ここからベクトルの議論に戻ります。
仕事とは、
「力」×「力の方向に移動した距離」
と、中学や高校で習いました。
例えば、3Nの力を物体に左向きに加えて、その結果左向きに4m進んだならば、
その仕事は3×4で、答えは12Jです(J(ジュールと読む)は、仕事の単位)
ところで、かばんをもって運んでいる・・・というように、
力は上向きだが、横に移動している場合は・・・
このとき、横向きに移動しているはずが、横向きには全く力が働いていないので、
よって仕事は0Jです。
ところで、力と、力の方向が直交しているとき、仕事は0J・・・
これはベクトルの内積になります。
つまり、仕事とは
「力」というベクトル量と
「移動した距離」というベクトル量の
内積なのです!
ほら、こんなところにもベクトルの知識が出てきました。 当然、内積はスカラーなので、
仕事(J)もスカラー量です。
仕事とは、
「力」×「力の方向に移動した距離」
と、中学や高校で習いました。
例えば、3Nの力を物体に左向きに加えて、その結果左向きに4m進んだならば、
その仕事は3×4で、答えは12Jです(J(ジュールと読む)は、仕事の単位)
ところで、かばんをもって運んでいる・・・というように、
力は上向きだが、横に移動している場合は・・・
このとき、横向きに移動しているはずが、横向きには全く力が働いていないので、
よって仕事は0Jです。
ところで、力と、力の方向が直交しているとき、仕事は0J・・・
これはベクトルの内積になります。
つまり、仕事とは
「力」というベクトル量と
「移動した距離」というベクトル量の
内積なのです!
ほら、こんなところにもベクトルの知識が出てきました。 当然、内積はスカラーなので、
仕事(J)もスカラー量です。
仕事の意味
仕事が12Jでした・・・って言われても、ねェ
仕事って一体、どのような量なのでしょうか?
少しの力を加えても物体がたくさん移動したならば、その仕事の値は大きくなります。
また、どんなに強い力を加えすぎて、例えあなたが疲れ果ててしまったとしても、肝心の物体が全く動かなければ、仕事は0です。
逆に、力を加えたが、逆に押し返されてしまった場合、力の向きと移動した距離が逆ということもあり、仕事の値は実はマイナスです!!!
はて、仕事の値の意味って・・・ますます分からなくなってきましたね?
どんなに疲れても、動かなければ結局0だし・・・
だから、仕事とエネルギー量とは一見全く関係ないように見えます。
しかし・・・仕事とエネルギーは、ものすごい深い関係があるのです。
仕事とは、「相手に与えたエネルギー」だと考えてください。
確かエネルギーとは、「運動エネルギー」と「位置エネルギー」の和でしたよね?(中学・高校物理)
力を加えても、全然動かなければ相手に与えた仕事は0です。
だって、高くなっているわけでもないし(位置エネルギーは増えていない)
速くなったわけでもないですから(運動エネルギーは増えていない)
また、力を加えたが押し返された時の、仕事がマイナスということは、
相手のエネルギーを減らしたことになります。
とりあえず、力を加えることで、手前に進む物体の抵抗をしたわけですから、
少なくとも速度は下がってます。(つまり運動エネルギーが減っている)
最後に、力を加えた向きに物体が進んでくれた場合、
力を加えているわけですから、物体は加速度運動をし、
力を加えるのをやめてもそのまま等速度運動するはずです。
よって物体は加速した(運動エネルギーが増えた)ので、仕事はプラスになります。
普通、速度$\displaystyle{v}$の物体の運動エネルギーは
$\displaystyle{\frac12mv^2}$
ですので、
もし12Jの仕事をした場合、
$\displaystyle{\frac12mv^2=12}$
という方程式を解けば、仕事を与えた後の速度が分かります。
・・・ところで、確かに仕事を与えたのに、力を加えるのをやめたら物体が止まってしまう(運動エネルギーが0になる)ことってありますよね?
このとき、その運動エネルギーは摩擦力によって熱エネルギーに変換されます。
「エネルギー保存の法則」という法則がありまして、
エネルギーは他のエネルギーに変換されて、決してなくなることはない、というのです。
この法則はすごいですね!!
現代の物理学では、この「エネルギー保存の法則」が破られたことは決してありません。
例えば、何かしらのエネルギーもなくなることはなく「化学エネルギー」「電気エネルギー」「光エネルギー」などなど、他のエネルギーにちゃんと変換されます。
※余談ですが、分子や原子のような、とても細かい世界(これをミクロな世界という)では、
先ほどの運動方程式F=maは成り立たなくなってしまいます。
つまり、ミクロな世界では、
我々が目で見ることのできる世界(マクロな世界という)とはまた違った物理現象が起きているのです。
その新しい物理学のことを量子力学といいます。
実は、「エネルギー保存の法則」は、このミクロな世界でも成立します。
すごいですね!!!
量子力学は、そのうちこのページでも解説していきたいな☆
これも余談ですが、
ところで、もし「エネルギーがなくならない」とかだったら、
現代社会の課題である「エネルギー問題」はすぐに解決されると思いませんか?
「省エネなんてする必要ないでしょ?だってエネルギーはなくならないんだもん」
と思うかもしれませんが・・・
実はそう簡単ではないのです。
「熱エネルギー」実はコイツは相当厄介ものであります。
熱エネルギーは、他のエネルギーにとても変換されにくいのです。
だから、地球温暖化とか、そいう問題が起きているのですね。
仕事って一体、どのような量なのでしょうか?
少しの力を加えても物体がたくさん移動したならば、その仕事の値は大きくなります。
また、どんなに強い力を加えすぎて、例えあなたが疲れ果ててしまったとしても、肝心の物体が全く動かなければ、仕事は0です。
逆に、力を加えたが、逆に押し返されてしまった場合、力の向きと移動した距離が逆ということもあり、仕事の値は実はマイナスです!!!
はて、仕事の値の意味って・・・ますます分からなくなってきましたね?
どんなに疲れても、動かなければ結局0だし・・・
だから、仕事とエネルギー量とは一見全く関係ないように見えます。
しかし・・・仕事とエネルギーは、ものすごい深い関係があるのです。
仕事とは、「相手に与えたエネルギー」だと考えてください。
確かエネルギーとは、「運動エネルギー」と「位置エネルギー」の和でしたよね?(中学・高校物理)
力を加えても、全然動かなければ相手に与えた仕事は0です。
だって、高くなっているわけでもないし(位置エネルギーは増えていない)
速くなったわけでもないですから(運動エネルギーは増えていない)
また、力を加えたが押し返された時の、仕事がマイナスということは、
相手のエネルギーを減らしたことになります。
とりあえず、力を加えることで、手前に進む物体の抵抗をしたわけですから、
少なくとも速度は下がってます。(つまり運動エネルギーが減っている)
最後に、力を加えた向きに物体が進んでくれた場合、
力を加えているわけですから、物体は加速度運動をし、
力を加えるのをやめてもそのまま等速度運動するはずです。
よって物体は加速した(運動エネルギーが増えた)ので、仕事はプラスになります。
普通、速度$\displaystyle{v}$の物体の運動エネルギーは
$\displaystyle{\frac12mv^2}$
ですので、
もし12Jの仕事をした場合、
$\displaystyle{\frac12mv^2=12}$
という方程式を解けば、仕事を与えた後の速度が分かります。
・・・ところで、確かに仕事を与えたのに、力を加えるのをやめたら物体が止まってしまう(運動エネルギーが0になる)ことってありますよね?
このとき、その運動エネルギーは摩擦力によって熱エネルギーに変換されます。
「エネルギー保存の法則」という法則がありまして、
エネルギーは他のエネルギーに変換されて、決してなくなることはない、というのです。
この法則はすごいですね!!
現代の物理学では、この「エネルギー保存の法則」が破られたことは決してありません。
例えば、何かしらのエネルギーもなくなることはなく「化学エネルギー」「電気エネルギー」「光エネルギー」などなど、他のエネルギーにちゃんと変換されます。
※余談ですが、分子や原子のような、とても細かい世界(これをミクロな世界という)では、
先ほどの運動方程式F=maは成り立たなくなってしまいます。
つまり、ミクロな世界では、
我々が目で見ることのできる世界(マクロな世界という)とはまた違った物理現象が起きているのです。
その新しい物理学のことを量子力学といいます。
実は、「エネルギー保存の法則」は、このミクロな世界でも成立します。
すごいですね!!!
量子力学は、そのうちこのページでも解説していきたいな☆
これも余談ですが、
ところで、もし「エネルギーがなくならない」とかだったら、
現代社会の課題である「エネルギー問題」はすぐに解決されると思いませんか?
「省エネなんてする必要ないでしょ?だってエネルギーはなくならないんだもん」
と思うかもしれませんが・・・
実はそう簡単ではないのです。
「熱エネルギー」実はコイツは相当厄介ものであります。
熱エネルギーは、他のエネルギーにとても変換されにくいのです。
だから、地球温暖化とか、そいう問題が起きているのですね。
持ち上げるとき
1gの物体には、約10Nの重力が働いています。
さて、これを3m上に持ち上げるときの重力に対して行った仕事はいくらになるでしょう。
たいていの教科書や参考書では、
10N×3m=30J
って書いてあります。。。
ってちょっと待って下さい?あれ?
確か、仕事は
「移動させた時の力」×「力の方向に移動した距離」
だったはずです。
「進行方向に対して抵抗した力」×「力の方向に移動した距離」
ではありません。
10Nの重力が働いたといっても、
実際に10Nで持ち上げた、ということについては、何も触れられていません。
だって、10Nの重力が働いている物体を上に3m持ち上げた、と言っても
真上に20Nの力で持ち上げたのかもしれません。
この時は、
20N×3m=60J
になります。
しつこいようですが、
10Nの重力が働いている物体を
10Nの力で持ち上げた、とは一言もいってません。
なのに、なんで
10N×3m=30J
なのでしょうか?
しかし、結論からいうと、
10Nの重力が働く物体を3m上に持ち上げたときの重力に対して行った仕事は、
確かに10N×3mで30Jなのです。
もし仮に、10Nよりも大きな力で持ち上げたとしましょう。
例えば11Nで持ち上げたとしましょうか?
このとき11N×3m=33Jの仕事を与えたことになりますが、
そうしたらこの物体には、
上向きに11N,下向きに重力10N働くことになり、
合力は上向きに1Nとなります。
1N残っているということは・・・この物体は加速していますよね?
だから、この物体を3m持ち上げた後も動き続けることになります。
つまり運動エネルギーが残っています。
11Nの力で持ち上げて、
33Jの仕事をこの物体に与えたとき、
重力に対して行った仕事30Jは位置エネルギーとなり、
残りの3Jは運動エネルギーになった、ということです。
さて、これを3m上に持ち上げるときの重力に対して行った仕事はいくらになるでしょう。
たいていの教科書や参考書では、
10N×3m=30J
って書いてあります。。。
ってちょっと待って下さい?あれ?
確か、仕事は
「移動させた時の力」×「力の方向に移動した距離」
だったはずです。
「進行方向に対して抵抗した力」×「力の方向に移動した距離」
ではありません。
10Nの重力が働いたといっても、
実際に10Nで持ち上げた、ということについては、何も触れられていません。
だって、10Nの重力が働いている物体を上に3m持ち上げた、と言っても
真上に20Nの力で持ち上げたのかもしれません。
この時は、
20N×3m=60J
になります。
しつこいようですが、
10Nの重力が働いている物体を
10Nの力で持ち上げた、とは一言もいってません。
なのに、なんで
10N×3m=30J
なのでしょうか?
しかし、結論からいうと、
10Nの重力が働く物体を3m上に持ち上げたときの重力に対して行った仕事は、
確かに10N×3mで30Jなのです。
もし仮に、10Nよりも大きな力で持ち上げたとしましょう。
例えば11Nで持ち上げたとしましょうか?
このとき11N×3m=33Jの仕事を与えたことになりますが、
そうしたらこの物体には、
上向きに11N,下向きに重力10N働くことになり、
合力は上向きに1Nとなります。
1N残っているということは・・・この物体は加速していますよね?
だから、この物体を3m持ち上げた後も動き続けることになります。
つまり運動エネルギーが残っています。
11Nの力で持ち上げて、
33Jの仕事をこの物体に与えたとき、
重力に対して行った仕事30Jは位置エネルギーとなり、
残りの3Jは運動エネルギーになった、ということです。