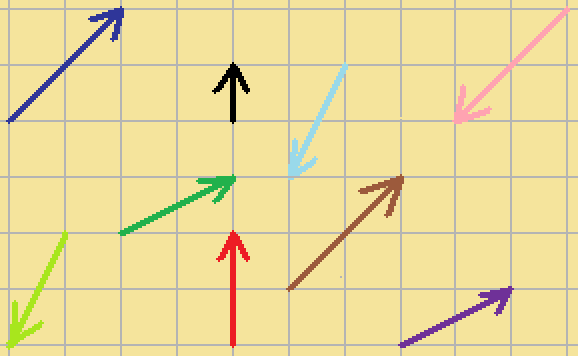
上の図で、
青のベクトルを$\displaystyle{\vec{a}}$
黄緑のベクトルを$\displaystyle{\vec{b}}$
黒のベクトルを$\displaystyle{\vec{c}}$
緑のベクトルを$\displaystyle{\vec{d}}$
赤のベクトルを$\displaystyle{\vec{e}}$
水色のベクトルを$\displaystyle{\vec{f}}$
茶色のベクトルを$\displaystyle{\vec{g}}$
ピンクのベクトルを$\displaystyle{\vec{h}}$
紫のベクトルを$\displaystyle{\vec{i}}$
とします。(見にくくてすみません😓 )

前回も説明しましたが、
ベクトルとは「大きさ」と「方向」を持つものです。
だから、大きさと方向が同じであれば、同じベクトルです。

例えば上の図の場合、
$\displaystyle{\vec{a}}$と$\displaystyle{\vec{g}}$は同じベクトルで、
$\displaystyle{\vec{a}=\vec{g}}$です。

「でも、矢印の位置は違いますが・・・」
いいえ、位置は関係ありません。
ベクトルは「大きさ」と「方向」さえ一緒であれば、同じベクトルとみなすのです。

「でも、青色と茶色って、色が違うから・・・」
ベクトルに色は全然関係ありません。
ベクトルは「大きさ」と「方向」さえ一緒であれば、色が違っていても位置が違っていても、同じベクトルとみなします。

「でも、青色のベクトル$\displaystyle{\vec{a}}$の方が、矢印の線が太く見える気が・・・」
ベクトルには線の太さは全然関係ありません！！！
方向と大きささえ同じであれば、いいのです(←しつこいかな？)

しかし、青のベクトル$\displaystyle{\vec{a}}$とピンクのベクトル$\displaystyle{\vec{h}}$ は違うベクトルです。
この二つ、大きさ(矢印の大きさ)は同じなのですが、
向きが違います。
$\displaystyle{\vec{a}}$と$\displaystyle{\vec{h}}$は、互いに逆の方向を向いています。
ベクトルは「大きさ」と「方向」の両方が同じでなければ「同じベクトル」とみなせないので、
この２つのベクトルは方向が１８０°違うため、同じベクトルではありません。


また、赤のベクトル$\displaystyle{\vec{c}}$と黒のベクトル$\displaystyle{\vec{e}}$ は方向が同じですが、大きさが違っているので、「同じベクトル」とはみなせません。




もしよければ、他にも同じベクトルのペアを自分で探してみてください。
全部で同じベクトルのペアは３組ありますねっ☆

ベクトルは「大きさ」と「方向」を表しますが・・・

大きさのない・・・つまり大きさが０のベクトルをゼロベクトルといい、
$\displaystyle{\vec{0}}$
と表します。

このベクトルを矢印で表そうとしても、ベクトルの大きさが０なので、
「矢印の長さ」も０になってしまう、つまり「ただの点」になってしまいます。
ただの点では、方向も表すことができないですね・・・。

よって、ゼロベクトルとは、方向も大きさも持たないベクトルなのですが、
それでも一応「ベクトル」と呼びます。