ベクトルの引き算
Follow @tepika_mathマイナスをつける
例えば$\displaystyle{3}$にマイナスをつけたら、$\displaystyle{-3}$になります。
また、$\displaystyle{-3}$にマイナスをつけたら$\displaystyle{3}$になります。
当たり前ですねf(^^;)
ベクトルにも、マイナスがついたりします。
たとえば、$\displaystyle{-\vec{a}}$ということにもなります。
ベクトルにマイナスがつくと、大きさはそのままですが、向きは逆になります。
例えば、
$\displaystyle{\vec{a}=}$
のとき、
$\displaystyle{-\vec{a}=}$
となります。
また、$\displaystyle{-3}$にマイナスをつけたら$\displaystyle{3}$になります。
当たり前ですねf(^^;)
ベクトルにも、マイナスがついたりします。
たとえば、$\displaystyle{-\vec{a}}$ということにもなります。
ベクトルにマイナスがつくと、大きさはそのままですが、向きは逆になります。
例えば、
$\displaystyle{\vec{a}=}$

のとき、
$\displaystyle{-\vec{a}=}$

となります。
ベクトルの引き算
前回は、ベクトルの足し算なるものを紹介しました。
同様にベクトルにも引き算の概念があります。
なんと偶然(?)にも、ベクトルの引き算にも2通りの方法があります。
それぞれ、「A−タイプ」「B−タイプ」としましょうか?
同様にベクトルにも引き算の概念があります。
なんと偶然(?)にも、ベクトルの引き算にも2通りの方法があります。
それぞれ、「A−タイプ」「B−タイプ」としましょうか?
A−タイプの考え方
基本的には、こっちの方が簡単です。
 $\displaystyle{-}$
$\displaystyle{-}$
ところで、普通の数の場合
$\displaystyle{x-y=x+(-y)}$
です。
つまり、引き算の場合、二番目の項の符号を変えて足し算をするのと同じことです。
それはベクトルでも同じで、
$\displaystyle{\vec{a}-\vec{b}=\vec{a}+(-\vec{b})}$
となります。
よって、
 $\displaystyle{-}$
$\displaystyle{-}$ $\displaystyle{=}$
$\displaystyle{=}$ $\displaystyle{-}$
$\displaystyle{-}$
となるので、あとは平行四辺形を作って解けばいいです。
ちなみに結果は以下の通りです。
 $\displaystyle{-}$
$\displaystyle{-}$ $\displaystyle{=}$
$\displaystyle{=}$
 $\displaystyle{-}$
$\displaystyle{-}$
ところで、普通の数の場合
$\displaystyle{x-y=x+(-y)}$
です。
つまり、引き算の場合、二番目の項の符号を変えて足し算をするのと同じことです。
それはベクトルでも同じで、
$\displaystyle{\vec{a}-\vec{b}=\vec{a}+(-\vec{b})}$
となります。
よって、
 $\displaystyle{-}$
$\displaystyle{-}$ $\displaystyle{=}$
$\displaystyle{=}$ $\displaystyle{-}$
$\displaystyle{-}$
となるので、あとは平行四辺形を作って解けばいいです。
ちなみに結果は以下の通りです。
 $\displaystyle{-}$
$\displaystyle{-}$ $\displaystyle{=}$
$\displaystyle{=}$
B−タイプの考え方
$\displaystyle{\vec{a}-\vec{b}}$の場合、
1.2つのベクトルの始点(矢印の最初の部分)、を揃えます。
2.$\displaystyle{\vec{b}}$の終点から、$\displaystyle{\vec{a}}$の終点まで、ベクトルをひきます。
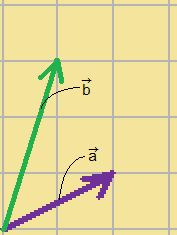
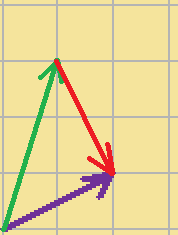
こうしてできた赤いベクトルが、
求めるベクトルです。
この方法で気をつけるべきことは、
第二項のベクトルの終点を、求めるベクトルの始点にすることです。
決して逆にベクトルをひかないでください!!!
当然ですが、「A−タイプ」も「B−タイプ」も同じ値が出ます。
1.2つのベクトルの始点(矢印の最初の部分)、を揃えます。
2.$\displaystyle{\vec{b}}$の終点から、$\displaystyle{\vec{a}}$の終点まで、ベクトルをひきます。


こうしてできた赤いベクトルが、
求めるベクトルです。
この方法で気をつけるべきことは、
第二項のベクトルの終点を、求めるベクトルの始点にすることです。
決して逆にベクトルをひかないでください!!!
当然ですが、「A−タイプ」も「B−タイプ」も同じ値が出ます。