外積の意味
Follow @tepika_math外積のノルムは?
前回は外積というものを紹介しました。
しかし、外積の計算は複雑なだけで、とても分かりにくいのでは・・・?
そこで今回は、外積というベクトル量が一体何を表しているのか説明します(^o^)/
まず、ベクトルの外積のノルム(長さのこと)は、一体どうなっているでしょうか?
とりあえず、そこから見ていきましょう。
実は、ベクトル$\displaystyle{\vec{a},\vec{b}}$の外積のノルムは
二つのベクトルのなす角度を$\displaystyle{\theta}$として、
$\displaystyle{\|\vec{a}\times\vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin\theta}$
となっています(余裕のあるのある人は、実際に計算して確かめてください)。
これって、高校数学の知識でも分かると思いますが、平行四辺形の面積ですよね?
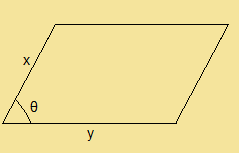
辺の長さがxとyで、角度θで挟まれた平行四辺形の面積は
$\displaystyle{xy\sin\theta}$
となります。
つまり、ベクトルの外積のノルムは、2つのベクトルで作られる平行四辺形の面積を表しています。
ここで、少し内積の確認もしていきます。
確認:
$\displaystyle{\vec{a}\cdot\vec{b} = \|\vec{a}| \|\vec{b}\| \cos\theta}$
$\displaystyle{\| \vec{a} \times \vec{b} \| = \|\vec{a}\| \|\vec{b}\| \sin\theta}$
こうしてみると、内積と外積って少し似てるような・・・?
しかし、外積の計算は複雑なだけで、とても分かりにくいのでは・・・?
そこで今回は、外積というベクトル量が一体何を表しているのか説明します(^o^)/
まず、ベクトルの外積のノルム(長さのこと)は、一体どうなっているでしょうか?
とりあえず、そこから見ていきましょう。
実は、ベクトル$\displaystyle{\vec{a},\vec{b}}$の外積のノルムは
二つのベクトルのなす角度を$\displaystyle{\theta}$として、
$\displaystyle{\|\vec{a}\times\vec{b}\| = \|\vec{a}\| \|\vec{b}\| \sin\theta}$
となっています(余裕のあるのある人は、実際に計算して確かめてください)。
これって、高校数学の知識でも分かると思いますが、平行四辺形の面積ですよね?

辺の長さがxとyで、角度θで挟まれた平行四辺形の面積は
$\displaystyle{xy\sin\theta}$
となります。
つまり、ベクトルの外積のノルムは、2つのベクトルで作られる平行四辺形の面積を表しています。
ここで、少し内積の確認もしていきます。
確認:
$\displaystyle{\vec{a}\cdot\vec{b} = \|\vec{a}| \|\vec{b}\| \cos\theta}$
$\displaystyle{\| \vec{a} \times \vec{b} \| = \|\vec{a}\| \|\vec{b}\| \sin\theta}$
こうしてみると、内積と外積って少し似てるような・・・?
外積の方向は?
外積によって作られたベクトルのノルムの大きさが、平行四辺形の面積を表していることが分かりました。
でも、2つのベクトルの外積はスカラーではなくベクトルです。
ノルムは分かりましたが、方向は一体どっちを向いているのでしょう…?
結論からいいますと、2つのベクトルから作られる平行四辺形に垂直な方向が、
実は外積の方向となっています。
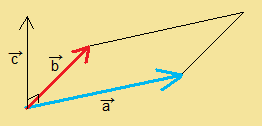
ベクトル$\displaystyle{\vec{a},\vec{b}}$の 外積の向きは、
ベクトル$\displaystyle{\vec{a},\vec{b}}$によって作られる 平行四辺形を通る平面に垂直な方向です。
でも、2つのベクトルの外積はスカラーではなくベクトルです。
ノルムは分かりましたが、方向は一体どっちを向いているのでしょう…?
結論からいいますと、2つのベクトルから作られる平行四辺形に垂直な方向が、
実は外積の方向となっています。

ベクトル$\displaystyle{\vec{a},\vec{b}}$の 外積の向きは、
ベクトル$\displaystyle{\vec{a},\vec{b}}$によって作られる 平行四辺形を通る平面に垂直な方向です。
あれっ?向きは?
ちょっと待った!!!
よ〜く考えてみると、垂直な向きって2つありませんか?
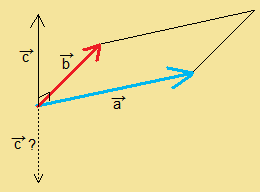
上向き?下向き?どっち???
これは、右手座標系or左手座標系によります。
右手座標系って・・・?(?_?)
まぁそれは後で詳しく説明するつもりですが・・・
ちらっと紹介をしましょう。
よ〜く考えてみると、垂直な向きって2つありませんか?

上向き?下向き?どっち???
これは、右手座標系or左手座標系によります。
右手座標系って・・・?(?_?)
まぁそれは後で詳しく説明するつもりですが・・・
ちらっと紹介をしましょう。
右手座標系&左手座標系
今までの数学では、座標を用いるときに、
x軸として、右向きを正に、左向きを負にしました。
y軸として、上向きを正に、下向きを負にしました。
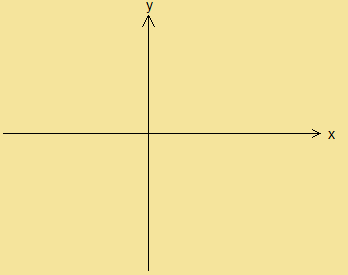
↑今までのグラフではこんなカンジでした
しかし、3次元の座標では、一体どっち向きを正の方向に持っていけばいいのでしょうか?
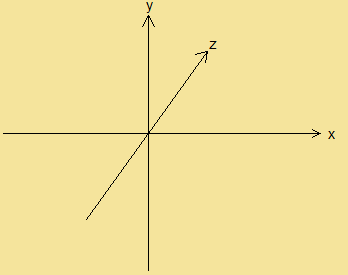
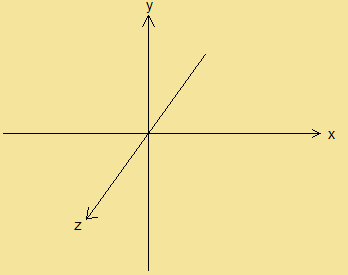
上の図では、左側はz軸は奥の方に、右側はz軸は手前の方を向いています。
例えば、(0,0,0)の1つ奥の位置の座標を(0,0,1)と置けばいいのか、
それとも(0,0,0)の1つ手前の位置の座標(0,0,1)と置けばいいのか・・・
ちなみに、左側の座標の取り方を左手座標系右側の座標の取り方を右手座標系といいます。
右手座標系・左手座標系、どちらがいいのかは、用途におまかせされています。
ところで、何故左手座標系と言うのかといえば・・・
中学の理科の実験でやった、「フレミングの左手の法則」の形をしてください!
親指をx軸、人差し指をy軸、中指をz軸とすると、たしかに指先が正の向きを向いていますよね?
ちなみに右手座標系は、「フレミングの右手の法則」の形をしたら、確かに正の向きになりますよね?
(できれば、手の図を書きたかった・・・)
ちなみに、コレ↓は右手座標系でしょうか?左手座標系でしょうか?
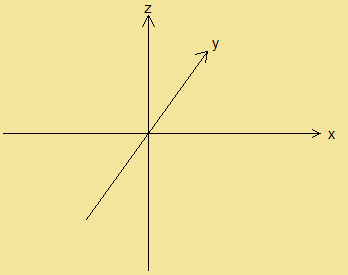
これは、なんとか頑張って手を回転して見ると、右手座標系になっていることが分かったでしょうか?
右手座標系と左手座標系は、ちょうど鏡で反転したような関係になっています。
x軸として、右向きを正に、左向きを負にしました。
y軸として、上向きを正に、下向きを負にしました。

↑今までのグラフではこんなカンジでした
しかし、3次元の座標では、一体どっち向きを正の方向に持っていけばいいのでしょうか?


上の図では、左側はz軸は奥の方に、右側はz軸は手前の方を向いています。
例えば、(0,0,0)の1つ奥の位置の座標を(0,0,1)と置けばいいのか、
それとも(0,0,0)の1つ手前の位置の座標(0,0,1)と置けばいいのか・・・
ちなみに、左側の座標の取り方を左手座標系右側の座標の取り方を右手座標系といいます。
右手座標系・左手座標系、どちらがいいのかは、用途におまかせされています。
ところで、何故左手座標系と言うのかといえば・・・
中学の理科の実験でやった、「フレミングの左手の法則」の形をしてください!
親指をx軸、人差し指をy軸、中指をz軸とすると、たしかに指先が正の向きを向いていますよね?
ちなみに右手座標系は、「フレミングの右手の法則」の形をしたら、確かに正の向きになりますよね?
(できれば、手の図を書きたかった・・・)
ちなみに、コレ↓は右手座標系でしょうか?左手座標系でしょうか?

これは、なんとか頑張って手を回転して見ると、右手座標系になっていることが分かったでしょうか?
右手座標系と左手座標系は、ちょうど鏡で反転したような関係になっています。
で、結局外積の向きは?
そうですね・・・右手座標系or左手座標系でベクトルの外積の向きもちがってきます。
ベクトルの外積の向きですが・・・
もし右手座標系だったら右手を、左手座標系だったら左手をご用意くださいm(_ _)m
例えば$\displaystyle{\vec{a}\times\vec{b}}$のとき、
ベクトル$\displaystyle{\vec{a}}$を親指に、
ベクトル$\displaystyle{\vec{b}}$を人差し指に合わせます。
そして、再びフレミングの法則の手の形をして、中指の指の方向が外積の方向となります。

これが右手座標系のときで、
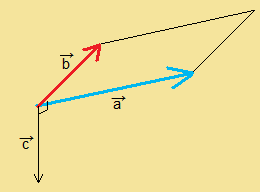
これが左手座標系のときです。
物理では、普通は右手座標系を用います。
(・・・やっぱり、図を使わないとうまく説明できなかったかなぁ??)
ベクトルの外積の向きですが・・・
もし右手座標系だったら右手を、左手座標系だったら左手をご用意くださいm(_ _)m
例えば$\displaystyle{\vec{a}\times\vec{b}}$のとき、
ベクトル$\displaystyle{\vec{a}}$を親指に、
ベクトル$\displaystyle{\vec{b}}$を人差し指に合わせます。
そして、再びフレミングの法則の手の形をして、中指の指の方向が外積の方向となります。

これが右手座標系のときで、

これが左手座標系のときです。
物理では、普通は右手座標系を用います。
(・・・やっぱり、図を使わないとうまく説明できなかったかなぁ??)