「ベクトルは材料です。その一次結合からどんどん新しいベクトルが作られます」
このことは一次結合の意味というページで述べたと思います。

実はベクトルの一次結合全体の集合は線形空間を成します！！！

以下、軽い証明です。
例えばベクトル$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合とは、
$\displaystyle{k_1v_1+k_2v_2+\cdots+k_nv_n}$の形のベクトルのことをいうのでした。



一方、以下が線形空間の定義でした。

1. $\displaystyle{\mathbb{0} \in V}$である。ここで$\displaystyle{\mathbb{0}}$はゼロベクトルとする
2. $\displaystyle{v_1,v_2 \in V}$ならば$\displaystyle{v_1+v_2 \in V}$
3. $\displaystyle{v \in V}$ならば、任意の実数$\displaystyle{c}$に対して$\displaystyle{cv \in V}$

条件1.は$\displaystyle{k_1=k_2=\cdots=k_n=0}$を代入してみましょう。
$\displaystyle{0v_1+0v_2+\cdots+0v_n}$は当然ゼロベクトルですよね？
このようにしてベクトルの一次結合から、なんとゼロベクトルが作れちゃうので、条件1.が示されました。



条件2.を示すために、
$\displaystyle{u=s_1v_1+s_2v_2+\cdots+s_nv_n}$
$\displaystyle{w=t_1v_1+t_2v_2+\cdots+t_nv_n}$
とします。ベクトル$\displaystyle{u,w}$は確かに$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合ですね。
そして$\displaystyle{u+w}$というベクトルも$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合となります。
実際、
$\displaystyle{u+w=(s_1v_1+s_2v_2+\cdots+s_nv_n)+(t_1v_1+t_2v_2+\cdots+t_nv_n)}$
$\displaystyle{=(s_1+t_1)v_1+(s_2+t_2)v_2+\cdots+(s_n+t_n)v_n}$
となりますよね。

はい、確かに$\displaystyle{u+w}$というベクトルも$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合であることが示されました。


条件3.は
$\displaystyle{v=k_1v_1+k_2v_2+\cdots+k_nv_n}$としたとき、
その定数倍である$\displaystyle{cv}$というベクトルも$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合であることを示します。
$\displaystyle{cv=ck_1v_1+ck_2v_2+\cdots+ck_nv_n}$と考えれば、
$\displaystyle{cv}$というベクトルも$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合であることが分かります。


以上より、ベクトル$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合全体からなるベクトルの集合は、線形空間であることが分かりました！！

「一次結合全体からなる集合」というのが、最も基本的な線形空間の例ではないでしょうか？

このように、ベクトルの組を適当に与えれば“一次結合”という操作により、線形空間が作れちゃいます☆

そういう意味で、ベクトルの組というのは、線形空間の“材料”であるということが、ご理解頂けたと思います。



一つのベクトルの線形結合の全体は“直線”という線形空間を表し・・・
二つの一次独立なベクトルの線形結合の全体は“平面”という線形空間を表し・・・
三つの一次独立なベクトルの線形結合の全体は“３次元空間”という線形空間を表し・・・
四つの一次独立なベクトルの線形結合の全体は“４次元超空間”という線形空間を表し・・・

線形空間$\displaystyle{V}$が 一次独立なベクトルの組$\displaystyle{v_1,v_2,\cdots,v_n}$の一次結合全体の集合であるとき、
$\displaystyle{v_1,v_2,\cdots,v_n}$は線形空間$\displaystyle{V}$の基底であると言います。




“基底”とは、英語で「ｂａｓｅ」と言います。
ということで「基底とは、線形空間の材料なんだな〜」って理解して頂ければ、幸いです(*^-^

上の図の青色からなる領域は、線形空間でした・・・てぃぅか、平面全体の集合ですねf(^ ^;

さて、この線形空間の基底を求めましょう。
「この線形空間は、一体どのベクトルを基底として成り立っているんだろう・・・」
ということを考えるのも必要です。


例えば、この平面空間は、
$\displaystyle{v_1=\begin{pmatrix}1\\0\end{pmatrix}}$
$\displaystyle{v_2=\begin{pmatrix}0\\1\end{pmatrix}}$
としたとき、２つのベクトル$\displaystyle{v_1,v_2}$を基底とした線形空間とも考えられますよね？



一方、
$\displaystyle{u_1=\begin{pmatrix}1\\0\end{pmatrix}}$
$\displaystyle{u_2=\begin{pmatrix}1\\1\end{pmatrix}}$
を基底とした線形空間とも考えられます。



実際確かめてみればよいと思うのですが、
$\displaystyle{v_1,v_2}$を基底とした線形空間と、 $\displaystyle{u_1,u_2}$を基底とした線形空間は全く同じ線形空間を描くことが分かります。



そうです！！
一つの線形空間に対して、とりうる基底はいくつかあるのです！！

次に

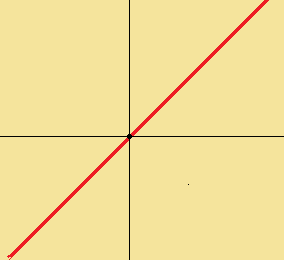
のような線形空間を考えましょう。

この線形空間の基底は
$\displaystyle{u=\begin{pmatrix}1\\1\end{pmatrix}}$
でも良いし、
$\displaystyle{v=\begin{pmatrix}{-2}\\{-2}\end{pmatrix}}$
でもよいです。


実際$\displaystyle{u}$を基底とした線形空間も $\displaystyle{v}$を基底とした線形空間も、全く同じ線形空間を描くことが分かります。