以下では全順序関係を持った 集合を考えますm(_ _)m

さてさて、今からこの全順序集合を
小さい組と
大きい組の
二組に分割することを考えます。


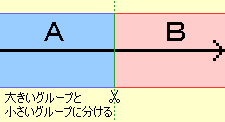
↑の図のように、大きい方を 小さい方をとします。

つまり、以下の条件を満たすようにを２つに分けるのですね。



つまり、
どんなの元も かのどちらか一方に必ず入っているように、
またよりの方が絶対大きくなるように
して、分割するのです。


この分割のことをの切断といい、

と書きます。
を上組 を下組といいます。

例えば整数の分割はどうなるでしょうか？


この一番目の例では、
上組を−１よりも以下の整数、 下組を０以上の整数としています。
また二番目の例では、
上組を３以下の整数、 下組を４以上の整数としています。
この２つは、切断になっています。



この２つは切断になっていませんね。
一番目の例では、０が上組と下組の両方に入っています。
二番目の例では、０が上・下組どちらにも入っていません。

切断は分かりましたか？

ところで切断には以下の４つのタイプがあることが知られています。

1. 上組に最小元が存在し、下組に最大元が存在する切断
2. 上組には最小元が存在せず、下組にも最大元が存在しない切断
3. 上組に最小元は存在するが、下組には最大値が存在しない
4. 上組には最小元が存在しないが、下組は最大元が存在する

例えば、整数は、必ず１．の切断しかできません。
整数をどのように上組・下組に切断しても、絶対に上組に最小元、下組に最大元が存在します。

と切断した場合、確かに下組には最大元−１、上組には最小元０がありますね？


それでは、有理数はどうでしょうか？
有理数は、２．３．４.の切断が可能ですが、
１．の切断はできません。

もし１．の切断ができたとして、その切断をとします。
そして の最大元と の最小元 とすると、
有理数は稠密であることにより、 と の間にまた別の数が存在するはずですが、それは切断の定義に矛盾します。
(↑はとどっちに含まれるの？という話になります。)




以上の３つの切断はそれぞれ、２．３．４．の条件を満たしています。
具体的に説明すると、
一番上の切断は、下組として√２より小さな有理数、上組として√２より大きい有理数の切断を意味しています。
一番上の切断は、下組として０より小さな有理数、上組として０以上の有理数の切断を意味しています。
一番上の切断は、下組として０以下の有理数、上組として０より大きい有理数の切断を意味しています。

次に気になるのは、実数の切断のことでしょうか？




から分かるように、
実数は絶対に３．４．の切断しかできません。



この切断では、√２が上組にも下組にも含まれないので、これは切断ではありません。
つまり２．の切断はどのようにやっても絶対にできないことが知られています。
（証明は、実数の定義に戻る必要があるので、ここでは省略します。むしろこの切断が実数の切断になっている？）


この性質のことを「実数の連続性」と呼んだりしますが・・・
このように(？)、実数の切断というのは結構重要なのでデデキント切断と呼ばれます。


まぁともかく、どうしても３．４．の切断しかできないような全順序集合のことを完備な順序集合といいます(汗)