全単射
Follow @tepika_math全単射
全射と単射は覚えてますか?
もし忘れてしまった方は、こちらをご覧くださいm(_ _)m→全射と単射
・・・さて、全射と単射はよろしいですね?
全射でも単射でもある写像のことを全単射と言います。
また、上への一対一の写像とも言います。
さて、以下の写像の例も全単射になります。
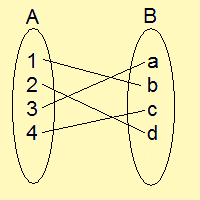
見て分かる通り、これは単射なため、終域、つまり$\displaystyle{\mathbb{B}}$の元は全て一つの逆像しか持ちません。
また、全射なため、終域の全ての元には絶対に逆像を持ちます。
これらのことをまとめると、全単射のとき「終域の全ての元は、必ずただ一つだけの逆像を持つ」ということが分かると思います。
つまり、全単射のときは逆像も写像となってしまいます!!
この場合、このようになると思いますよ♪
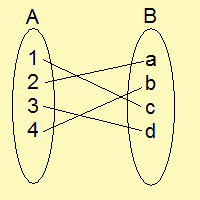
このように写像の逆像をとって、新たに作った写像のことを逆写像といいます。
逆写像となるには、元の写像が全単射であることが必要です!!
もし元の写像が全射でなかった場合、終域に逆像のないものが存在してしまいます。これは「写像は全ての始域の元にはただ一つの対応が存在する」という定義に反します。
また、元の写像が単射でなかった場合には、終域の逆像が複数存在してしまうことがあるため、これも写像の定義に反します。
もし忘れてしまった方は、こちらをご覧くださいm(_ _)m→全射と単射
・・・さて、全射と単射はよろしいですね?
全射でも単射でもある写像のことを全単射と言います。
また、上への一対一の写像とも言います。
さて、以下の写像の例も全単射になります。

見て分かる通り、これは単射なため、終域、つまり$\displaystyle{\mathbb{B}}$の元は全て一つの逆像しか持ちません。
また、全射なため、終域の全ての元には絶対に逆像を持ちます。
これらのことをまとめると、全単射のとき「終域の全ての元は、必ずただ一つだけの逆像を持つ」ということが分かると思います。
つまり、全単射のときは逆像も写像となってしまいます!!
この場合、このようになると思いますよ♪

このように写像の逆像をとって、新たに作った写像のことを逆写像といいます。
逆写像となるには、元の写像が全単射であることが必要です!!
もし元の写像が全射でなかった場合、終域に逆像のないものが存在してしまいます。これは「写像は全ての始域の元にはただ一つの対応が存在する」という定義に反します。
また、元の写像が単射でなかった場合には、終域の逆像が複数存在してしまうことがあるため、これも写像の定義に反します。
置換
今度は、
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
を考えましょう。また、fは全単射であるとします。
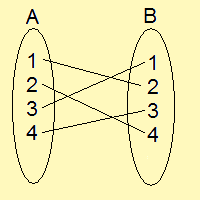
のような時、全単射を以下のように表したりします。
$\displaystyle{\begin{pmatrix}1&2&3&4\\2&4&1&3\end{pmatrix}}$
気をつけてください。これは行列と表記が同じですが、行列ではありません。
全単射を表したものだと思ってください。
上側の要素は始域を、下側の要素は終域を表しています。
この全単射の表記のことを置換といいます。
またこの全単射の逆像は、
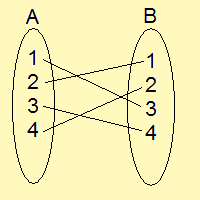
となるので、
$\displaystyle{\begin{pmatrix}1&2&3&4\\2&4&1&3\end{pmatrix}^{-1}=\begin{pmatrix}1&2&3&4\\3&1&4&2\end{pmatrix}}$
となります。
ところで、左辺の右上の-1は、この置換(写像)の逆像を表しています。
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
を考えましょう。また、fは全単射であるとします。

のような時、全単射を以下のように表したりします。
$\displaystyle{\begin{pmatrix}1&2&3&4\\2&4&1&3\end{pmatrix}}$
気をつけてください。これは行列と表記が同じですが、行列ではありません。
全単射を表したものだと思ってください。
上側の要素は始域を、下側の要素は終域を表しています。
この全単射の表記のことを置換といいます。
またこの全単射の逆像は、

となるので、
$\displaystyle{\begin{pmatrix}1&2&3&4\\2&4&1&3\end{pmatrix}^{-1}=\begin{pmatrix}1&2&3&4\\3&1&4&2\end{pmatrix}}$
となります。
ところで、左辺の右上の-1は、この置換(写像)の逆像を表しています。