写像
Follow @tepika_math写像
$\displaystyle{\mathbb{A}=\{1,2,3,4,5\}}$
$\displaystyle{\mathbb{B}=\{a,b,c,d\}}$
があり、それが以下のように対応づけされているとします。
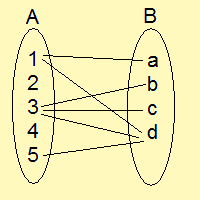
この図を見て分かるように、5はdに対応されていますが、
中には1や3のように、対応先が複数あるものもあります。
また、2や4には何も対応されていません。
しかし、対応というものは、このようなものでも実は許されます。
それでは、次の対応を見てみましょう。
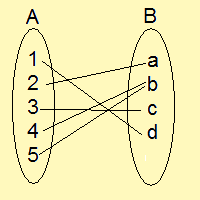
今度は、全ての$\displaystyle{\mathbb{A}}$の元は、 それぞれただ一つだけの$\displaystyle{\mathbb{B}}$の元に対応されています。
前の対応の例みたいに、対応先が複数あるとか、対応先のない元があるとかいうものはありません。
このように、各始域の元に対応先が絶対に1つだけ存在し、対応先のないものが存在しないような関係のことを写像といいます。
写像はとても重要なので、是非覚えておきましょう。
関数は写像の一種です。
例えば、
$\displaystyle{f(x)=x^2}$ のような具体的な例を出してみると、関数とは始域が実数で終域も実数である写像、つまり
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
と考えることができませんか?
特に始域、終域が複素数であるもの、
$\displaystyle{f:\mathbb{C}\rightarrow\mathbb{C}}$
は複素関数と呼ばれます。
また、
$\displaystyle{f(x,y)=x^2+y^2}$のような2変数関数も、
$\displaystyle{f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}}$
と考えれば、写像になることが分かると思います。 と考えれば、写像になることが分かると思います。
$\displaystyle{\mathbb{B}=\{a,b,c,d\}}$
があり、それが以下のように対応づけされているとします。

この図を見て分かるように、5はdに対応されていますが、
中には1や3のように、対応先が複数あるものもあります。
また、2や4には何も対応されていません。
しかし、対応というものは、このようなものでも実は許されます。
それでは、次の対応を見てみましょう。

今度は、全ての$\displaystyle{\mathbb{A}}$の元は、 それぞれただ一つだけの$\displaystyle{\mathbb{B}}$の元に対応されています。
前の対応の例みたいに、対応先が複数あるとか、対応先のない元があるとかいうものはありません。
このように、各始域の元に対応先が絶対に1つだけ存在し、対応先のないものが存在しないような関係のことを写像といいます。
写像はとても重要なので、是非覚えておきましょう。
関数は写像の一種です。
例えば、
$\displaystyle{f(x)=x^2}$ のような具体的な例を出してみると、関数とは始域が実数で終域も実数である写像、つまり
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
と考えることができませんか?
特に始域、終域が複素数であるもの、
$\displaystyle{f:\mathbb{C}\rightarrow\mathbb{C}}$
は複素関数と呼ばれます。
また、
$\displaystyle{f(x,y)=x^2+y^2}$のような2変数関数も、
$\displaystyle{f:\mathbb{R}\times\mathbb{R}\rightarrow\mathbb{R}}$
と考えれば、写像になることが分かると思います。 と考えれば、写像になることが分かると思います。
写像の表し方
写像$\displaystyle{f}$に$\displaystyle{x}$を入れたら$\displaystyle{y}$が出てくる時、
つまり$\displaystyle{f(x)=y}$のとき、
$\displaystyle{f:x{\mapsto}y}$
と記述することがあります。
例えば写像$\displaystyle{f}$を
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
$\displaystyle{f(x)=x^2}$
とします。
こうすると
$\displaystyle{f:x{\mapsto}x^2}$
ですね。
つまり$\displaystyle{f(x)=y}$のとき、
$\displaystyle{f:x{\mapsto}y}$
と記述することがあります。
例えば写像$\displaystyle{f}$を
$\displaystyle{f:\mathbb{R}\rightarrow\mathbb{R}}$
$\displaystyle{f(x)=x^2}$
とします。
こうすると
$\displaystyle{f:x{\mapsto}x^2}$
ですね。
部分写像

この例では、1と3は複数の元に対応しており、2と4は対応先が存在しないため、写像ということができませんでした。
しかし、5は1つの元に対応しております。
よって、始域、つまり$\displaystyle{\mathbb{A}}$の部分集合である{5}を考えたら、写像になることができます。
このように、始域の部分集合(この部分集合のことを定義域と呼ぶ)が写像になっているときは、この対応は部分写像と呼びます。
だから、この集合$\displaystyle{\mathbb{A}}$から集合$\displaystyle{\mathbb{B}}$への対応は写像ではないですが、部分写像にはなっていますよね?
無理矢理写像で表す
上の例は部分写像となりますが、写像にはなりませんでした。
しかし$\displaystyle{\mathbb{A}}$から$\displaystyle{\mathbb{B}}$への対応ではなく、
$\displaystyle{f:\mathbb{A}\rightarrow\mathfrak{P}(\mathbb{B})}$を考えれば、一応写像にならないでしょうか?
ところで$\displaystyle{\mathfrak(\mathbb{B})}$は$\displaystyle{\mathbb{B}}$の冪集合です。
$\displaystyle{\mathbb{B}}$の冪集合とは、$\displaystyle{\mathbb{B}}$の部分集合を全て集めたものです。(詳しくはコチラ☆)
例えば、1と3は複数の元に対応してますが、そこで
$\displaystyle{f(1)=\{a,d\}}$
$\displaystyle{f(3)=\{b,c,d\}}$
というように、1つの集合へ対応させるようにすれば、写像になりますよね?
ちなみに、2と4は、空集合に対応させればよいと思います。
また、
$\displaystyle{f(5)=\{d\}}$
のように、5のような1つの元に対応させるようなものも、集合に対応させなければならなくなることにも気をつけましょう。
しかし$\displaystyle{\mathbb{A}}$から$\displaystyle{\mathbb{B}}$への対応ではなく、
$\displaystyle{f:\mathbb{A}\rightarrow\mathfrak{P}(\mathbb{B})}$を考えれば、一応写像にならないでしょうか?
ところで$\displaystyle{\mathfrak(\mathbb{B})}$は$\displaystyle{\mathbb{B}}$の冪集合です。
$\displaystyle{\mathbb{B}}$の冪集合とは、$\displaystyle{\mathbb{B}}$の部分集合を全て集めたものです。(詳しくはコチラ☆)
例えば、1と3は複数の元に対応してますが、そこで
$\displaystyle{f(1)=\{a,d\}}$
$\displaystyle{f(3)=\{b,c,d\}}$
というように、1つの集合へ対応させるようにすれば、写像になりますよね?
ちなみに、2と4は、空集合に対応させればよいと思います。
また、
$\displaystyle{f(5)=\{d\}}$
のように、5のような1つの元に対応させるようなものも、集合に対応させなければならなくなることにも気をつけましょう。