触点
Follow @tepika_math触点の定義
$\displaystyle{A}$を位相空間$\displaystyle{X}$の部分集合とします。
$\displaystyle{p{\in}X}$として、
$\displaystyle{U_p}$を、点$\displaystyle{p}$の任意の近傍とします(←任意の“開近傍”でもよい)。
このとき$\displaystyle{U_p}$と$\displaystyle{A}$の共通部分が空集合でないとき、
つまり$\displaystyle{U_p{\cap}A{\neq}\phi}$のとき、
$\displaystyle{p}$は$\displaystyle{A}$の触点であると言います。
$\displaystyle{p{\in}X}$として、
$\displaystyle{U_p}$を、点$\displaystyle{p}$の任意の近傍とします(←任意の“開近傍”でもよい)。
このとき$\displaystyle{U_p}$と$\displaystyle{A}$の共通部分が空集合でないとき、
つまり$\displaystyle{U_p{\cap}A{\neq}\phi}$のとき、
$\displaystyle{p}$は$\displaystyle{A}$の触点であると言います。
分かりにくい定義です
確かに、分かりにくい定義(ていうか、少々ややこしい)ですけどね・・・(‾д‾;)
初学者には、この定義はややこいしく感じてしまうのでしょうか?
毎度のごとく、以下に例を挙げますので、
定義をしっかりと覚えて、残りのページにを読むことに励んでくださいませm(_ _)m
初学者には、この定義はややこいしく感じてしまうのでしょうか?
毎度のごとく、以下に例を挙げますので、
定義をしっかりと覚えて、残りのページにを読むことに励んでくださいませm(_ _)m
例1
実数$\displaystyle{\mathbb{R}}$通常の位相(ユークリッド位相)を考えましょう。

例えば、$\displaystyle{\mathbb{R}}$の元$\displaystyle{1}$は、開区間$\displaystyle{(1,3)}$の触点になっています。
このことを調べるために、まず$\displaystyle{1}$の近傍を考えてみましょう。

上の図のように、
$\displaystyle{1}$の、どのような小さな開近傍をとっても、
どうしても、厚みができてしまいます。(上の図では、その厚みを$\displaystyle{\varepsilon}$で表しています)
その$\displaystyle{\varepsilon}$の厚みが、どうしても開区間$\displaystyle{(1,3)}$に浸食してしまうのです。

例えば、$\displaystyle{\mathbb{R}}$の元$\displaystyle{1}$は、開区間$\displaystyle{(1,3)}$の触点になっています。
このことを調べるために、まず$\displaystyle{1}$の近傍を考えてみましょう。

上の図のように、
$\displaystyle{1}$の、どのような小さな開近傍をとっても、
どうしても、厚みができてしまいます。(上の図では、その厚みを$\displaystyle{\varepsilon}$で表しています)
その$\displaystyle{\varepsilon}$の厚みが、どうしても開区間$\displaystyle{(1,3)}$に浸食してしまうのです。
例2
じゃぁ、$\displaystyle{0}$は開区間$\displaystyle{(1,3)}$の触点でしょうか???

以下のように、

0の近傍$\displaystyle{(-1,2)}$を取ります。
確かにこうすれば$\displaystyle{(1,3)}$と共通部分を持つ0の近傍も存在するのですが・・・
以下の例を見て下さい。
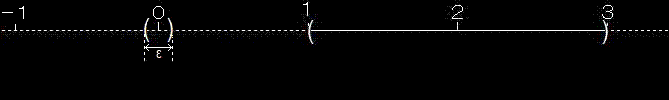
$\displaystyle{(-\varepsilon,\varepsilon)}$という0の近傍は$\displaystyle{(1,3)}$と交わっていません。
よって$\displaystyle{0}$は$\displaystyle{(1,3)}$の触点ではないです。
$\displaystyle{0}$の近傍が絶対に$\displaystyle{(1,3)}$と交わっているならば、 $\displaystyle{0}$は$\displaystyle{(1,3)}$の触点と言えたのですが、
$\displaystyle{(-\varepsilon,\varepsilon)}$というような例外が1つでも存在してしまったら、
これは“触点”とは言わないのです。

以下のように、

0の近傍$\displaystyle{(-1,2)}$を取ります。
確かにこうすれば$\displaystyle{(1,3)}$と共通部分を持つ0の近傍も存在するのですが・・・
以下の例を見て下さい。
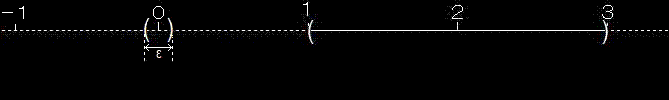
$\displaystyle{(-\varepsilon,\varepsilon)}$という0の近傍は$\displaystyle{(1,3)}$と交わっていません。
よって$\displaystyle{0}$は$\displaystyle{(1,3)}$の触点ではないです。
$\displaystyle{0}$の近傍が絶対に$\displaystyle{(1,3)}$と交わっているならば、 $\displaystyle{0}$は$\displaystyle{(1,3)}$の触点と言えたのですが、
$\displaystyle{(-\varepsilon,\varepsilon)}$というような例外が1つでも存在してしまったら、
これは“触点”とは言わないのです。
例3
たとえば$\displaystyle{A}$を位相空間$\displaystyle{X}$の部分集合とします。
$\displaystyle{a{\in}A}$のとき、
$\displaystyle{a}$は$\displaystyle{A}$の触点になります。
だって$\displaystyle{a}$の任意の近傍$\displaystyle{U_a}$は、絶対に$\displaystyle{a}$を含んでいる↓
$\displaystyle{a{\in}U_a}$
ので、当然$\displaystyle{U_a}$と$\displaystyle{A}$には交わりはあります。
具体的にしますと、
0,1,2はいずれも閉区間$\displaystyle{[0,2]}$の触点になります。
$\displaystyle{a{\in}A}$のとき、
$\displaystyle{a}$は$\displaystyle{A}$の触点になります。
だって$\displaystyle{a}$の任意の近傍$\displaystyle{U_a}$は、絶対に$\displaystyle{a}$を含んでいる↓
$\displaystyle{a{\in}U_a}$
ので、当然$\displaystyle{U_a}$と$\displaystyle{A}$には交わりはあります。
具体的にしますと、
0,1,2はいずれも閉区間$\displaystyle{[0,2]}$の触点になります。
少し説明
ここで、もう一度“触点”の定義の確認です!!
$\displaystyle{x}$が$\displaystyle{A}$の触点とは↓↓↓
$\displaystyle{x}$のどんな近傍も絶対に$\displaystyle{A}$と交わる!!!
$\displaystyle{x}$が$\displaystyle{A}$の触点の直感的なイメージとして、
「$\displaystyle{x}$は$\displaystyle{A}$に触れているorくっついている」
という言い方がふさわしいのでしょうか???
$\displaystyle{x}$の近傍とは、$\displaystyle{x}$を含む、厚みのある領域(範囲?)のことです。
(まだ、近傍という言葉が分からない人は、「近傍」を「開集合」と置き換えてもいいです。)
$\displaystyle{x}$が$\displaystyle{A}$にくっついているとは、
「どんな$\displaystyle{x}$の近傍も、その厚みのせいで$\displaystyle{A}$と交わってしまうこと」をいうのです。
例えば、先ほどの例で
「$\displaystyle{0}$は$\displaystyle{(1,3)}$の触点ではない」
と述べましたが、
それは$\displaystyle{0}$と$\displaystyle{(1,3)}$の間には十分な間隔があるため、
$\displaystyle{0}$の近傍、つまり“隙間”を上手く調整すれば、$\displaystyle{(1,3)}$にぶつからなくてすむ、というわけです。
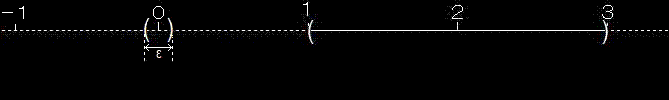
上の場合、とりあえず1よりも小さな$\displaystyle{\epsilon}$という厚みをもった隙間を選んで、$\displaystyle{(1,3)}$と交わらないように、調整しています。
一方、$\displaystyle{1}$は$\displaystyle{(1,3)}$の触点となってしまいます。

上の図のように、どんな小さな厚みをとっても$\displaystyle{(1,3)}$にぶつかってしまうため、これは触点となってしまうわけですね。
当然ですが、1より大きくて3より小さい数は、必ず$\displaystyle{(1,3)}$の触点になっています。
これは先ほどの例3で見たことですね。
$\displaystyle{A}$の任意の元は、必ず$\displaystyle{A}$の触点です。
$\displaystyle{A}$に含まれていない元が果たして触点なのかどうかに、議論の価値があるのですね。
$\displaystyle{x}$が$\displaystyle{A}$の触点とは↓↓↓
$\displaystyle{x}$のどんな近傍も絶対に$\displaystyle{A}$と交わる!!!
$\displaystyle{x}$が$\displaystyle{A}$の触点の直感的なイメージとして、
「$\displaystyle{x}$は$\displaystyle{A}$に触れているorくっついている」
という言い方がふさわしいのでしょうか???
$\displaystyle{x}$の近傍とは、$\displaystyle{x}$を含む、厚みのある領域(範囲?)のことです。
(まだ、近傍という言葉が分からない人は、「近傍」を「開集合」と置き換えてもいいです。)
$\displaystyle{x}$が$\displaystyle{A}$にくっついているとは、
「どんな$\displaystyle{x}$の近傍も、その厚みのせいで$\displaystyle{A}$と交わってしまうこと」をいうのです。
例えば、先ほどの例で
「$\displaystyle{0}$は$\displaystyle{(1,3)}$の触点ではない」
と述べましたが、
それは$\displaystyle{0}$と$\displaystyle{(1,3)}$の間には十分な間隔があるため、
$\displaystyle{0}$の近傍、つまり“隙間”を上手く調整すれば、$\displaystyle{(1,3)}$にぶつからなくてすむ、というわけです。
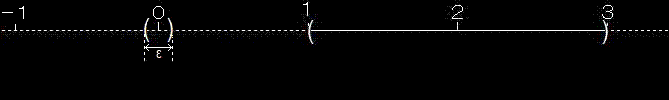
上の場合、とりあえず1よりも小さな$\displaystyle{\epsilon}$という厚みをもった隙間を選んで、$\displaystyle{(1,3)}$と交わらないように、調整しています。
一方、$\displaystyle{1}$は$\displaystyle{(1,3)}$の触点となってしまいます。

上の図のように、どんな小さな厚みをとっても$\displaystyle{(1,3)}$にぶつかってしまうため、これは触点となってしまうわけですね。
当然ですが、1より大きくて3より小さい数は、必ず$\displaystyle{(1,3)}$の触点になっています。
これは先ほどの例3で見たことですね。
$\displaystyle{A}$の任意の元は、必ず$\displaystyle{A}$の触点です。
$\displaystyle{A}$に含まれていない元が果たして触点なのかどうかに、議論の価値があるのですね。