内部・外部・境界
Follow @tepika_math境界の例
$\displaystyle{d(x,y)}$を$\displaystyle{\mathbb{R}^2}$のユークリッド距離として、
$\displaystyle{S=\{a|d(a,O)\geq\delta\}}$という領域を考えます。
ただし、$\displaystyle{O}$を原点とします。つまり$\displaystyle{O=(0,0)}$です。
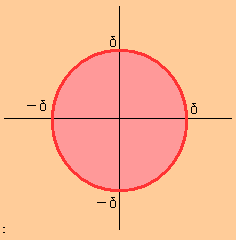
$\displaystyle{S}$とは、上の図で桃色と赤色を合わせた部分ですね。
つまり$\displaystyle{S}$は半径$\displaystyle{\delta}$の境界を含んだ円の領域のことです。
さてさて、領域$\displaystyle{S}$の境界は、赤色の線ですよね。
また、$\displaystyle{S}$の内部は桃色の部分であり、
$\displaystyle{S}$の外部は黄色の領域です。
いま「境界」「内部」「外部」という用語を何気なく使いましたが、
それらの言葉の定義は?
これが、このページのメインテーマになります(^^)
以下では「境界」「内部」「外部」という用語を、直感的なものに頼らずに、数学的に、きちんと厳密に定義したいと思います。
$\displaystyle{S=\{a|d(a,O)\geq\delta\}}$という領域を考えます。
ただし、$\displaystyle{O}$を原点とします。つまり$\displaystyle{O=(0,0)}$です。

$\displaystyle{S}$とは、上の図で桃色と赤色を合わせた部分ですね。
つまり$\displaystyle{S}$は半径$\displaystyle{\delta}$の境界を含んだ円の領域のことです。
さてさて、領域$\displaystyle{S}$の境界は、赤色の線ですよね。
また、$\displaystyle{S}$の内部は桃色の部分であり、
$\displaystyle{S}$の外部は黄色の領域です。
いま「境界」「内部」「外部」という用語を何気なく使いましたが、
それらの言葉の定義は?
これが、このページのメインテーマになります(^^)
以下では「境界」「内部」「外部」という用語を、直感的なものに頼らずに、数学的に、きちんと厳密に定義したいと思います。
内部とは
前回“内点”というのをやりましたね?
$\displaystyle{X}$を位相空間として、
$\displaystyle{A{\subset}X}$とします。
さて、$\displaystyle{A}$の内点を全て集めた集合を $\displaystyle{A}$の内部あるいは開核と言い、
$\displaystyle{A^{\circ}}$とか$\displaystyle{A^{i}}$とか$\displaystyle{\mathrm{Int}(A)}$と表します。
$\displaystyle{X}$を位相空間として、
$\displaystyle{A{\subset}X}$とします。
さて、$\displaystyle{A}$の内点を全て集めた集合を $\displaystyle{A}$の内部あるいは開核と言い、
$\displaystyle{A^{\circ}}$とか$\displaystyle{A^{i}}$とか$\displaystyle{\mathrm{Int}(A)}$と表します。
内部の例
例えば、
$\displaystyle{[0,1)}$の内部は、
$\displaystyle{[0,1)^{i}=(0,1)}$
となります。
$\displaystyle{0}$という元は$\displaystyle{[0,1)}$の内点ではありません。
“内点”に関することは、前回やりました。
よって$\displaystyle{[0,1)}$の内部というのは、0だけが除外されて
$\displaystyle{(0,1)}$となるのですよ。
$\displaystyle{[0,1)}$の内部は、
$\displaystyle{[0,1)^{i}=(0,1)}$
となります。
$\displaystyle{0}$という元は$\displaystyle{[0,1)}$の内点ではありません。
“内点”に関することは、前回やりました。
よって$\displaystyle{[0,1)}$の内部というのは、0だけが除外されて
$\displaystyle{(0,1)}$となるのですよ。
外部・境界
$\displaystyle{A}$の補集合の内点を$\displaystyle{A}$の外点といいます。
$\displaystyle{A}$の外点をすべて集めた集合を$\displaystyle{A}$の外部といいます。
$\displaystyle{A}$の内部でも外部でもない元を全て集めた集合を$\displaystyle{A}$の境界といいます。
ところで・・・「補集合って何だったっけ・・・(-.-)」っていう方はいらっしゃいませんか???
補集合に関することはココのページを見てください。
$\displaystyle{A}$の補集合は$\displaystyle{\overline{A}}$と書くのでしたね。
そして、$\displaystyle{A}$の補集合は$\displaystyle{\overline{A}=X-A}$となります。
(↑注:ところで、$\displaystyle{A}$の補集合として$\displaystyle{A^{C}}$と書き表すこともありますが、
この「位相」のページでは、補集合として$\displaystyle{A^{C}}$という記法は、採用しないものとします。)
$\displaystyle{A}$の外点をすべて集めた集合を$\displaystyle{A}$の外部といいます。
$\displaystyle{A}$の内部でも外部でもない元を全て集めた集合を$\displaystyle{A}$の境界といいます。
ところで・・・「補集合って何だったっけ・・・(-.-)」っていう方はいらっしゃいませんか???
補集合に関することはココのページを見てください。
$\displaystyle{A}$の補集合は$\displaystyle{\overline{A}}$と書くのでしたね。
そして、$\displaystyle{A}$の補集合は$\displaystyle{\overline{A}=X-A}$となります。
(↑注:ところで、$\displaystyle{A}$の補集合として$\displaystyle{A^{C}}$と書き表すこともありますが、
この「位相」のページでは、補集合として$\displaystyle{A^{C}}$という記法は、採用しないものとします。)
外部・境界の例
$\displaystyle{[0,1)}$の外部を考えたいと思います。
外部を求めるには、まず補集合から考えなければなりませんねっ☆
$\displaystyle{[0,1)}$の補集合は、
$\displaystyle{\overline{[0,1)}=\mathbb{R}-[0,1)=(-\infty,0)\cup[1,\infty)}$です。
次に、$\displaystyle{(-\infty,0)\cup[1,\infty)}$の内部を求めましょう。
$\displaystyle{(-\infty,0)\cup[1,\infty)}$の内部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$です。
つまり$\displaystyle{(-\infty,0)\cup[1,\infty)}$から$\displaystyle{1}$が除外されています。
よって$\displaystyle{[0,1)}$の外部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$となります。
また、$\displaystyle{A}$の境界とは、
$\displaystyle{A}$の内部でも外部でもない部分でしたから…
$\displaystyle{[0,1)}$の内部は$\displaystyle{(0,1)}$でした。
$\displaystyle{[0,1)}$の外部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$でした。
残りの部分、つまり$\displaystyle{\{0,1\}}$が$\displaystyle{[0,1)}$の境界となります。
まとめますと、
$\displaystyle{[0,1)}$の内部→$\displaystyle{(0,1)}$
$\displaystyle{[0,1)}$の外部→$\displaystyle{(-\infty,0)\cup(1,\infty)}$
$\displaystyle{[0,1)}$の境界→$\displaystyle{\{0,1\}}$

上の図の数直線で、
実線が$\displaystyle{[0,1)}$の内部
点線が$\displaystyle{[0,1)}$の外部
緑色の点が$\displaystyle{[0,1)}$の境界となります。
このように、位相空間の任意の元は“内部”“外部”“境界”と、3つの部分に、すっぱりと分かれるわけです。
外部を求めるには、まず補集合から考えなければなりませんねっ☆
$\displaystyle{[0,1)}$の補集合は、
$\displaystyle{\overline{[0,1)}=\mathbb{R}-[0,1)=(-\infty,0)\cup[1,\infty)}$です。
次に、$\displaystyle{(-\infty,0)\cup[1,\infty)}$の内部を求めましょう。
$\displaystyle{(-\infty,0)\cup[1,\infty)}$の内部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$です。
つまり$\displaystyle{(-\infty,0)\cup[1,\infty)}$から$\displaystyle{1}$が除外されています。
よって$\displaystyle{[0,1)}$の外部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$となります。
また、$\displaystyle{A}$の境界とは、
$\displaystyle{A}$の内部でも外部でもない部分でしたから…
$\displaystyle{[0,1)}$の内部は$\displaystyle{(0,1)}$でした。
$\displaystyle{[0,1)}$の外部は$\displaystyle{(-\infty,0)\cup(1,\infty)}$でした。
残りの部分、つまり$\displaystyle{\{0,1\}}$が$\displaystyle{[0,1)}$の境界となります。
まとめますと、
$\displaystyle{[0,1)}$の内部→$\displaystyle{(0,1)}$
$\displaystyle{[0,1)}$の外部→$\displaystyle{(-\infty,0)\cup(1,\infty)}$
$\displaystyle{[0,1)}$の境界→$\displaystyle{\{0,1\}}$

上の図の数直線で、
実線が$\displaystyle{[0,1)}$の内部
点線が$\displaystyle{[0,1)}$の外部
緑色の点が$\displaystyle{[0,1)}$の境界となります。
このように、位相空間の任意の元は“内部”“外部”“境界”と、3つの部分に、すっぱりと分かれるわけです。
二次元平面の円の例

さて、このページの冒頭で紹介した、
$\displaystyle{S=\{a|d(a,O)\geq\delta\}}$
↑の内部・外部・境界はどうなるでしょうか?
とりあえず、円周上の点(赤色の線)は$\displaystyle{S}$の内点ではありません。
円周上の点を含む開集合は、どうしても$\displaystyle{S}$をはみでてしまいます。
また、また赤色の線は外部でもないことも、明らかではないでしょうか?
よって、内部でもなく、外部でもない・・・つまり“境界”であることが分かりました。
このように、“境界”というのを、数学的な言葉を用いて表しているのです。