これからは、
２次元平面のことを$\displaystyle{\mathbb{R}^2}$と表し、
３次元空間のことを$\displaystyle{\mathbb{R}^3}$と表します。



ところで、実数全体の集合を$\displaystyle{\mathbb{R}}$と表すことは、覚えていますか？
$\displaystyle{\mathbb{R}^2}$とは一体何かと言いますと、
$\displaystyle{\mathbb{R}\times\mathbb{R}}$のこと、
つまり$\displaystyle{\mathbb{R}}$と$\displaystyle{\mathbb{R}}$の直積です。

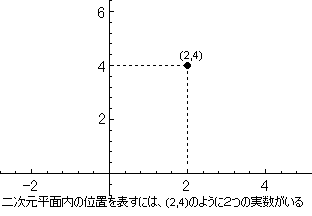
中学や高校以来、二次元平面で位置を表すときには、
点(２，４)みたいな、座標を用いて位置を表したと思います。
座標を２つの実数の組と考えたら、
「座標」というものは実数$\displaystyle{\mathbb{R}}$と$\displaystyle{\mathbb{R}}$の直積だと考えてもいいはずです。

・・・ということもあり、二次元平面は一般的に$\displaystyle{\mathbb{R}^2}$と表します。
(「直積」は集合論でやりましたよ・・・ね？)



同様に、三次元空間内の座標は、(３，−１，２）のような、
ｘ軸ｙ軸ｚ軸の３つの数を用いて位置を表しますので、
三次元空間は実数$\displaystyle{\mathbb{R}}$の３つの直積、つまり
$\displaystyle{\mathbb{R}\times\mathbb{R}\times\mathbb{R}}$
と考えられます。
だから、３次元空間は$\displaystyle{\mathbb{R}^3}$と表されます。

境界を含まない円のことを開円と言います。
例えば、
$\displaystyle{\{x|d(x,a){\lt}r\}}$
のような、点ａからの距離がｒより小さい領域は開円です。
ところで、$\displaystyle{d(x,a)}$はxとaの距離を表しています。



それでは、以前と同様に$\displaystyle{\mathbb{R}^2}$上での内点というものを定義したいと思います。
$\displaystyle{\mathbb{A}\subset\mathbb{R}^2}$とします。
$\displaystyle{p}$を、ある$\displaystyle{\mathbb{A}}$の元として、
$\displaystyle{p}$が$\displaystyle{\mathbb{A}}$の内点とは、
$\displaystyle{p{\in}S_p\subset\mathbb{A}}$となるような、開円$\displaystyle{S_p}$が存在するということです。


もし、全ての$\displaystyle{\mathbb{A}}$の元が$\displaystyle{\mathbb{A}}$の内点となるとき、
$\displaystyle{\mathbb{A}}$を開集合といい、
開集合の補集合のことを閉集合と言います。


ただ、今までの内点の定義が、
「開区間が存在する」→「開円が存在する」
というように、変わっただけですね？

まず、開円自体は当然開集合です。
$\displaystyle{p\in{S_p}\subset\mathbb{A}}$
のとき、$\displaystyle{S_p}$を開円に選べばいいのです。


ところで、直線や線分・曲線などの線は開集合になりません。
線上の点をどこにとっても線が開円に収まることはなく、はみ出てしまうからです。




また、１次元では境界(両端)を持つ区間は開集合ではないのと同様に、
２次元、つまり$\displaystyle{\mathbb{R}^2}$上の開集合では 境界を含む領域は開集合になりません。



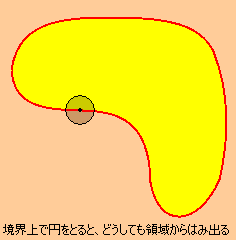
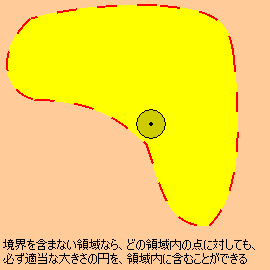
しかし、もし境界を含まない領域でしたら、１次元と同様に開集合になります。

前回は、実数$\displaystyle{\mathbb{R}}$上の区間で、
「開集合の公理」というものが、成り立つということを紹介しました。


$\displaystyle{\mathbb{R}^2}$平面でも、当然開集合の公理が成立します。

［Ｏ₁］ 全体集合(この場合、実数$\displaystyle{\mathbb{R}}$)と空集合$\displaystyle{\phi}$は開集合である

［Ｏ₂］ 開集合の任意個の和集合も開集合である

［Ｏ₃］ 開集合の有限個の共通部分も開集合である

$\displaystyle{\mathbb{R}^2}$平面で、上の公理が成り立つことの証明は、
前回の実数$\displaystyle{\mathbb{R}}$の場合と同様に示すことができます。


※注：これを示すには、実は「２つの開円の共通部分は開集合である(→証明)」という性質を使わなければ証明できませんね。

$\displaystyle{\mathbb{R}^3}$空間(３次元空間)の開集合も、
$\displaystyle{\mathbb{R}^2}$平面の場合と同様に定義できます。



$\displaystyle{\mathbb{R}^2}$で“開円”を用いたならば、
今度は$\displaystyle{\mathbb{R}^3}$では開球を用いればよいのです！！！


開円が境界を含まない円だったのに対し、
開球は境界を含まない(当然３次元の)球のことです。

同様に、内点の定義も、
「開区間が存在する」→「開円が存在する」→「開球が存在する」
に変わるだけです。


そして内点を定義して開集合を定義する所も、 また、開集合の公理も成り立つ所も
$\displaystyle{\mathbb{R}^2}$とほとんど同じです。