内積とベクトルの長さ
Follow @tepika_math内積を使ってベクトルの長さを求める
さて、前回までは内積を紹介しました。
この内積を使って、ベクトルの長さを求めることができます!!!
「ベクトルの長さなんて、矢印の長さなんだから、定規(?)みたいなもので測ればいいじゃん?」
なんて思うかもしれませんが、
ベクトルの長さを求めるのは、時と場合により、そう簡単じゃないことがあります。
そこで、以下にベクトルの長さを求める公式を書きます!!!
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}|^2}$
どうですか?
この公式によると、自分自身とのベクトルの内積が、自身のベクトルの2乗の値になるのです!!
しかし、確かにこの公式を始めてみた時は「?」と思うかもしれません。
この公式は、
「長さが分からないが、内積の値は一応分かるよ!!」
ってな時に使えます。
・・・ってそんなシュチュエーションって本当にあるの!?
と思うかもしれませんが、実は案外あります。
この内積を使って、ベクトルの長さを求めることができます!!!
「ベクトルの長さなんて、矢印の長さなんだから、定規(?)みたいなもので測ればいいじゃん?」
なんて思うかもしれませんが、
ベクトルの長さを求めるのは、時と場合により、そう簡単じゃないことがあります。
そこで、以下にベクトルの長さを求める公式を書きます!!!
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}|^2}$
どうですか?
この公式によると、自分自身とのベクトルの内積が、自身のベクトルの2乗の値になるのです!!
しかし、確かにこの公式を始めてみた時は「?」と思うかもしれません。
この公式は、
「長さが分からないが、内積の値は一応分かるよ!!」
ってな時に使えます。
・・・ってそんなシュチュエーションって本当にあるの!?
と思うかもしれませんが、実は案外あります。
もう少し詳しくみてみる
ベクトルの内積の定義によれば、
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}||\vec{a}|\cos\theta}$
となるはずですが、
$\displaystyle{\vec{a}}$と$\displaystyle{\vec{a}}$、つまり同じベクトルの内積なので、
その2つのベクトルのなす角は0°ですので、 $\displaystyle{\theta=0}$より$\displaystyle{\cos\theta=1}$です。
よって
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}||\vec{a}|\cos0^{\circ}=|\vec{a}|^2}$
となるわけです。
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}||\vec{a}|\cos\theta}$
となるはずですが、
$\displaystyle{\vec{a}}$と$\displaystyle{\vec{a}}$、つまり同じベクトルの内積なので、
その2つのベクトルのなす角は0°ですので、 $\displaystyle{\theta=0}$より$\displaystyle{\cos\theta=1}$です。
よって
$\displaystyle{\vec{a}\cdot\vec{a}=|\vec{a}||\vec{a}|\cos0^{\circ}=|\vec{a}|^2}$
となるわけです。
例
例えば、
$\displaystyle{|\vec{a}|=3}$
$\displaystyle{|\vec{b}|=4}$
として、2つのベクトルのなす角を、60°とします。
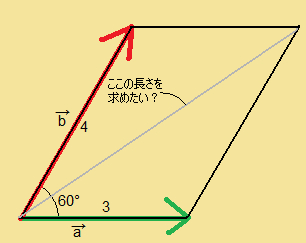
さて、この灰色の線である、対角線の長さを求めたいとき、どうすればいいでしょうか?
この灰色の長さを求めるには
$\displaystyle{|\vec{a}+\vec{b}|}$
を求めればいいのですが・・・
上の内積の公式を使いますと、
$\displaystyle{|\vec{a}+\vec{b}|^2}$
$\displaystyle{=(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b})}$
$\displaystyle{=|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2}$
となりました。
ところで、上の式の2行目から3行目の式は内積の性質を使いました。詳しくはココをご参照ください。
ここで、
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta}$なので、
$\displaystyle{|\vec{a}+\vec{b}|^2}$
$\displaystyle{=3^2+2\times6+4^2}$
$\displaystyle{=37}$
です。
つまり
$\displaystyle{|\vec{a}+\vec{b}|^2=37}$
となります。
しかし、37という数は、対角線の長さの2乗です。
だから平方根をとらなければなりませんね?
37の平方根は
$\displaystyle{\pm\sqrt{37}}$
ですが、「長さ」はマイナスにはならないので、
$\displaystyle{|\vec{a}+\vec{b}|=\sqrt{37}}$
です。
こうして、一見求まりにくそうな対角線の長さが分かりましたね。
$\displaystyle{|\vec{a}|=3}$
$\displaystyle{|\vec{b}|=4}$
として、2つのベクトルのなす角を、60°とします。

さて、この灰色の線である、対角線の長さを求めたいとき、どうすればいいでしょうか?
この灰色の長さを求めるには
$\displaystyle{|\vec{a}+\vec{b}|}$
を求めればいいのですが・・・
上の内積の公式を使いますと、
$\displaystyle{|\vec{a}+\vec{b}|^2}$
$\displaystyle{=(\vec{a}+\vec{b})\cdot(\vec{a}+\vec{b})}$
$\displaystyle{=|\vec{a}|^2+2\vec{a}\cdot\vec{b}+|\vec{b}|^2}$
となりました。
ところで、上の式の2行目から3行目の式は内積の性質を使いました。詳しくはココをご参照ください。
ここで、
$\displaystyle{\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta}$なので、
$\displaystyle{|\vec{a}+\vec{b}|^2}$
$\displaystyle{=3^2+2\times6+4^2}$
$\displaystyle{=37}$
です。
つまり
$\displaystyle{|\vec{a}+\vec{b}|^2=37}$
となります。
しかし、37という数は、対角線の長さの2乗です。
だから平方根をとらなければなりませんね?
37の平方根は
$\displaystyle{\pm\sqrt{37}}$
ですが、「長さ」はマイナスにはならないので、
$\displaystyle{|\vec{a}+\vec{b}|=\sqrt{37}}$
です。
こうして、一見求まりにくそうな対角線の長さが分かりましたね。