以前にも述べたように、ベクトルとは「大きさ」と「向き」を持ったものです。
例えば、

このベクトルの長さは１になります。

また、

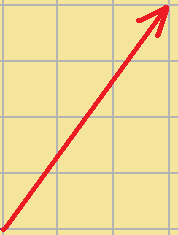
このベクトルの長さは５ですね。
(↑三平方の定理を使いました)。


ベクトル$\displaystyle{\vec{a}}$の長さは $\displaystyle{|\vec{a}|}$と表されます。


だから、
$\displaystyle{\vec{a}=}$
$\displaystyle{\vec{b}=}$
のとき、それぞれ
$\displaystyle{|\vec{a}|=1}$
$\displaystyle{|\vec{b}|=5}$
となります。

また、ゼロベクトルのとき、
$\displaystyle{|\vec{0}|=0}$
となるのは分かると思います。



・・・一つだけ注意点を述べます。
ベクトルの長さは絶対０以上の数になります。
例えば、
$\displaystyle{\vec{c}=}$
のとき、つまり$\displaystyle{\vec{c}}$が$\displaystyle{\vec{a}}$のちょうど反対向きのベクトルだったとします。

それでも、
$\displaystyle{|\vec{c}|=1}$
です。
当たり前かもしれませんが、反対向きのベクトルだからといって、 $\displaystyle{|\vec{c}|=-1}$とだけはしないように。。。

$\displaystyle{\vec{c}=}$
とします。

このとき、$\displaystyle{a}$を普通の数として、
ベクトル$\displaystyle{\vec{c}}$の$\displaystyle{a}$倍、つまり
$\displaystyle{a\vec{c}}$
は、向きはそのままで、長さを$\displaystyle{a}$倍に引き延ばしたベクトルになります。

例えば、
$\displaystyle{2\vec{c}=}$


当然、
$\displaystyle{\vec{d}=}$
とすると、
$\displaystyle{0.5\vec{d}}$

となります。

また、
$\displaystyle{-2\vec{c}}$
のように、ベクトルにマイナスの数をかけると、向きが逆になります。

ベクトルの引き算のページで、ベクトルにマイナスをつけると向きが逆になることを話しましたが、
「マイナスをつける→−１倍する」
と考えれば、話がつながると思います。


当然ですが、ベクトルを０倍したら、ゼロベクトルになります。